题目内容
【题目】设数列{an}的前n项和Sn满足Sn＝
，且a1，a2＋1，a3成等差数列．
（1）求数列{an}的通项公式；
（2）记数列
的前n项和为Tn，求证：
Tn＜1．
【答案】（1）
；（2）见解析
【解析】
（Ⅰ）由已知数列递推式得到an=2an﹣1（n≥2），再由已知a1，a2+1，a3成等差数列求出数列首项，可得数列{an}是首项为2，公比为2的等比数列，则其通项公式可求；
（Ⅱ）由（Ⅰ）求出数列
的通项公式，再由等比数列的前n项和求得T，再利用单调性求出T
的范围.
(1)由已知Sn＝2an－a1，有an＝Sn－Sn－1＝2an－2an－1(n≥2)，即an＝2an－1(n≥2)．从而a2＝2a1，a3＝2a2＝4a1.
又因为a1，a2＋1，a3成等差数列，即a1＋a3＝2(a2＋1)，所以a1＋4a1＝2(2a1＋1)，解得a1＝2.
所以数列{an}是首项为2，公比为2的等比数列．
故an＝2n.
(2)由(1)得
＝
，所以Tn＝
＋
＋…＋＝
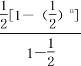＝1－.
由1－.在自然数集上递增，可得n=1时取得最小值
，
且1－＜1，
则≤Tn＜1．
练习册系列答案
相关题目
