题目内容
【题目】设椭圆E： 
（a＞b＞0）的左、右焦点F1、F2 ， 其离心率e= 
，且点F2到直线 
=1的距离为 
．
（1）求椭圆E的方程；
（2）设点P（x0 ， y0）是椭圆E上的一点（x0≥1），过点P作圆（x+1）2+y2=1的两条切线，切线与y轴交于A、B两点，求|AB|的取值范围．
【答案】
（1）
解：设F1（﹣c，0），F2（c，0），
依题意有 
， 
．
又∵a2=b2+c2，∴c=1，a=2，b= 
，
∴椭圆E的方程为： 
．
（2）
解：如图设圆的切线PM的方程为y=k（x﹣x0）+y0
由圆心（﹣1，0）到PM的距离为1，
|y0﹣k（x0+1）|= 
（x02+2x0）k2﹣2y0（x0+1）k+y02﹣1=0
令y=k（x﹣x0）+y0中x=0，y=y0﹣kx0
∴A（0，y0﹣kx0）．
设圆的切线PN的方程为y=k1（x﹣x0）+y0．
同理可得B（0，y0﹣k1x0）
依题意k1，k是方程（x02+2x0）k2﹣2y0（x0+1）k+y02﹣1=0的两个实根，
k1+k= 
，k1k= 
|AB|2=[x0（k﹣k1）]2= 
= 
．
∵ 
，∴|AB|2=1+ 
=1+ 
∵1≤x0≤2，∴|AB|2=1+ 
．
∴|AB|的取值范围为[ 
]
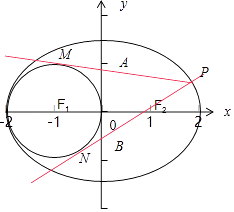
【解析】（1）设F1（﹣c，0），F2（c，0），依题意有 ， ．可得c=1，a=2，b= ， （2）如图设圆的切线PM的方程为y=k（x﹣x0）+y0 ， 由圆心（﹣1，0）到PM的距离为1，|y0﹣k（x0+1）|= （x02+2x0）k2﹣2y0（x0+1）k+y02﹣1=0，A（0，y0﹣kx0）．设圆的切线PN的方程为y=k1（x﹣x0）+y0 ， 同理可得B（0，y0﹣k1x0），依题意k1 ， k是方程（x02+2x0）k2﹣2y0（x0+1）k+y02﹣1=0的两个实根，|AB|2=[x0（k﹣k1）]2= = ．由 ，得|AB|2=1+ =1+ ．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
