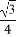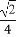题目内容
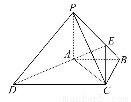
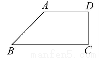
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=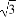 AD,E为CD上一点,且CE=3DE.
AD,E为CD上一点,且CE=3DE.

(1)求证:AE⊥平面SBD.
(2)M,N分别为线段SB,CD上的点,是否存在M,N,使MN⊥CD且MN⊥SB,若存在,确定M,N的位置;若不存在,说明理由.
(1)见解析 (2) 存在,理由见解析
【解析】(1)因为四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,
所以SD⊥平面ABCD.
BD就是SB在底面ABCD上的射影.
∵AB=2AD,E为CD上一点,且CE=3DE.
∴tan∠DAE=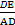 =
=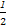 ,tan∠DBA=
,tan∠DBA=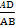 =
=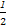 ,
,
∴∠DAE=∠DBA,同理∠BDA=∠AED,
∴∠DAE+∠BDA=90°.
∴AE⊥BD,∴AE⊥SB.∵SB∩BD=B,
∴AE⊥平面SBD.
(2)假设存在MN满足MN⊥CD且MN⊥SB.
建立如图所示的空间直角坐标系,

由题意可知,D(0,0,0),A(a,0,0),C(0,2a,0),B(a,2a,0),S(0,0,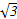 a),
a),
设 =
= +t
+t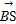 =(a,2a,0)+t(-a,-2a,
=(a,2a,0)+t(-a,-2a,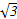 a)=(a-ta,2a-2ta,
a)=(a-ta,2a-2ta,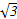 ta)(t∈[0,1]),
ta)(t∈[0,1]),
即M (a-ta,2a-2ta,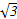 ta),N(0,y,0),y∈[0,2a],
ta),N(0,y,0),y∈[0,2a],
 =(a-ta,2a-2ta-y,
=(a-ta,2a-2ta-y,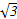 ta).
ta).
使MN⊥CD且MN⊥SB,
则

可得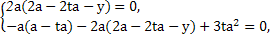
t=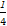 ∈[0,1],y=
∈[0,1],y=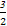 a∈[0,2a].
a∈[0,2a].
故存在MN使MN⊥CD且MN⊥SB.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目