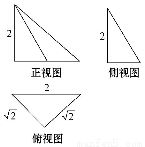
题目内容
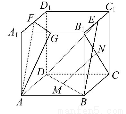
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC,点E是棱PB上的动点.
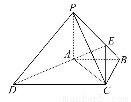
(1)若PD∥平面EAC,试确定点E在棱PB上的位置.
(2)在(1)的条件下,求二面角A-CE-P的余弦值.
(1) PE= PB (2)
PB (2) 
【解析】(1)在梯形ABCD中,由题知AB⊥BC,AB=BC,∴AC= AB,∠BAC=
AB,∠BAC= ,
,
∴∠DCA=∠BAC= .
.
又∠CAD=90°,
∴△DAC为等腰直角三角形.
∴DC= AC=
AC= (
( AB)=2AB.
AB)=2AB.
连接BD,交AC于点M,连接ME,

∵AB∥DC,∴ =
= =2.
=2.
∵PD∥平面EAC,
又平面EAC∩平面PDB=ME,
∴PD∥EM.
在△BPD中, =
= =2,∴PE=2EB,
=2,∴PE=2EB,
∴当PE= PB时,PD∥平面EAC.
PB时,PD∥平面EAC.
(2)由题意知△PAB为等腰直角三角形,取PB中点N,连接AN,则AN⊥PB.
∵PA⊥平面ABCD,∴PA⊥BC.
∵∠ABC=90°,即AB⊥BC,
又PA∩AB=A,∴BC⊥平面PAB.
∵BC?平面PCB,∴平面PAB⊥平面PCB,
又平面PAB∩平面PCB=PB,∴AN⊥平面PBC.
∵CE?平面PBC,∴AN⊥CE.
在平面PBC内,过点N作NH垂直直线CE于点H,连接AH.
∵AN⊥CE,NH⊥CE,AN∩NH=N,
∴CE⊥平面ANH,
∴AH⊥CE.∴∠AHN是二面角A-CE-P的平面角.
设PA=AB=BC=a,
则PB= =
= a,BE=
a,BE= PB=
PB= a,
a,
NE= PB-BE=
PB-BE= PB-
PB- PB=
PB= PB=
PB= a,
a,
CE= =
= a.
a.
∵NH⊥CE,EB⊥CB,∠NEH=∠CEB,
∴△NEH∽△CEB,∴ =
= ,
,
∴NH= =
= a.
a.
∵AN⊥平面PBC,NH?平面PBC,
∴AN⊥NH,则△AHN为直角三角形.
在Rt△AHN中,AN= AB=
AB= a,
a,
∴tan∠AHN= =
= ,
,
∴cos∠AHN= =
= =
= .
.
∴二面角A-CE-P的余弦值为 .
.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案