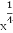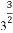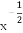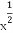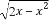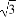题目内容
直三棱柱ABC-A1B1C1的底面为等腰直角三角形,∠BAC=90°,AB=AC=2,AA1=2 ,E,F分别是BC,AA1的中点.
,E,F分别是BC,AA1的中点.
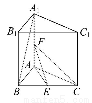
求(1)异面直线EF和A1B所成的角.
(2)三棱锥A-EFC的体积.
(1) 30° (2) 
【解析】(1)取AB的中点D,连DE,DF,则DF∥A1B,
∴∠DFE(或其补角)即为所求.
由题意易知,DF=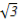 ,DE=1,AE=
,DE=1,AE=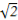 ,
,
由DE⊥AB,DE⊥AA1得DE⊥平面ABB1A1,
∴DE⊥DF,即△EDF为直角三角形,
∴tan∠DFE= =
=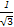 =
= ,∴∠DFE=30°,
,∴∠DFE=30°,
即异面直线EF和A1B所成的角为30°.
(2)VA-EFC=VF-AEC=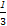 ·S△AEC·FA=
·S△AEC·FA=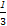 ×
× ×
×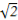 ×
×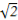 ×
×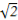 =
= .
.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目