题目内容
(本题满分15分) 如图,椭圆C: x2+3y2=3b2 (b>0).
(Ⅰ) 求椭圆C的离心率;
(Ⅱ) 若b=1,A,B是椭圆C上两点,且| AB | =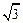 ,求△AOB面积的最大值.
,求△AOB面积的最大值.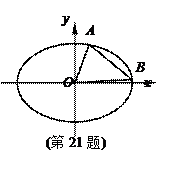
(Ⅰ)解:由x2+3y2=3b2 得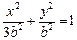 ,
,
所以e=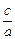 =
=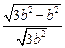 =
=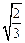 =
=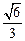 .
.
(Ⅱ)解:设A(x1,y1),B(x2,y2),△ABO的面积为S.
如果AB⊥x轴,由对称性不妨记A的坐标为( ,
, ),此时S=
),此时S=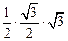 =
=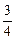 ;
;
如果AB不垂直于x轴,设直线AB的方程为y=kx+m,
由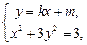 得x2+3(kx+m) 2=3,
得x2+3(kx+m) 2=3,
即 (1+3k2)x2+6kmx+3m2-3=0,又Δ=36k2m2-4(1+3k2) (3m2-3)>0,
所以 x1+x2=-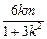 ,x1x2=
,x1x2=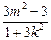 ,
,
(x1-x2)2=(x1+x2)2-4 x1x2=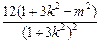 , ①
, ①
由 | AB |=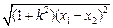 及 | AB |=
及 | AB |=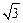 得
得
(x1-x2)2=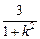 , ②
, ②
结合①,②得m2=(1+3k2)-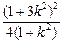 .又原点O到直线AB的距离为
.又原点O到直线AB的距离为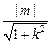 ,
,
所以S=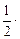
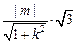 ,
,
因此S2=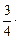
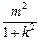 =
=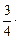 [
[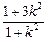 -
-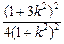 ]=
]=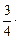 [-
[-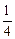 (
(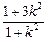 -2)2+1]
-2)2+1]
=-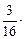 (
(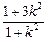 -2)2+
-2)2+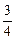 ≤
≤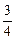 ,
,
故S≤ .当且仅当
.当且仅当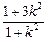 =2,即k=±1时上式取等号.又
=2,即k=±1时上式取等号.又 >
>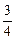 ,故S max=
,故S max= .
.
解析

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
极坐标系中,以(9, )为圆心,9为半径的圆的极坐标方程为( )
)为圆心,9为半径的圆的极坐标方程为( )
A.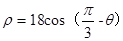 | B.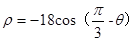 |
C.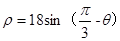 | D.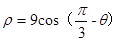 |
 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点
 ,且
,且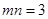 .
. 与
与 交点的轨迹
交点的轨迹 的方程;
的方程;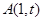 (
( )是轨迹
)是轨迹 是轨迹
是轨迹 的斜率
的斜率 与直线
与直线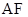 的斜率
的斜率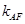 满足
满足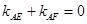 ,试探究直线
,试探究直线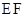 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
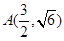 是曲线C1和C2的交点.
是曲线C1和C2的交点.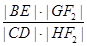 是否为定值,若是,求出定值;若不是,请说明理由.
是否为定值,若是,求出定值;若不是,请说明理由.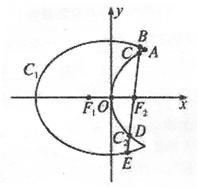
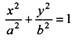 (a〉b>0)的左焦点为
(a〉b>0)的左焦点为 ,椭圆过点P(
,椭圆过点P(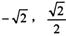 )
) 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
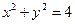 上任取一点
上任取一点 ,过点
,过点 轴的垂线段
轴的垂线段 ,
,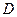 为垂足.当点
为垂足.当点 形成轨迹
形成轨迹 .
.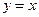 与曲线
与曲线 两点,
两点,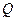 为曲线
为曲线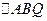 面积的最大值
面积的最大值 圆
圆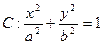 ,
,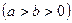 的离心率为
的离心率为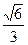 ,直线
,直线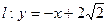 与以
与以 原点为圆心,以椭圆
原点为圆心,以椭圆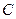 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。 、求椭圆
、求椭圆 、过点
、过点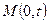 的直线
的直线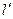 (斜率存在时)与椭圆
(斜率存在时)与椭圆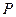 、
、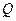 两点,设
两点,设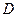 为椭圆
为椭圆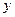 轴负半轴的交点,且
轴负半轴的交点,且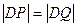 ,求实数
,求实数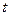 的取值范围。
的取值范围。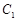 是以原点O为中心、
是以原点O为中心、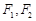 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线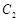 是以O为顶点、
是以O为顶点、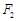 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线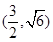 且
且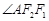 为钝角.
为钝角. 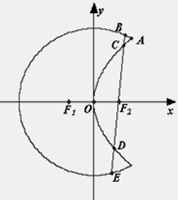
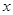 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线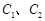 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问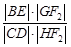 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.