题目内容
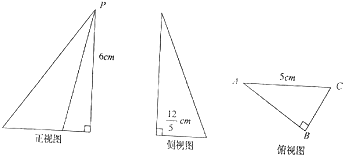 一几何体的三视图如图:
一几何体的三视图如图:(I)画出它的直观图,并求其体积;
(II)你能发现该几何体的哪些面互相垂直?试一一列出并说明理由.
分析:(I)结合三视图,直接画出它的直观图,利用并求其体积;
(II)通过直线与平面垂直,判断平面与平面垂直一一列出并说明理由.
(II)通过直线与平面垂直,判断平面与平面垂直一一列出并说明理由.
解答: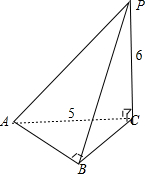 解:(I)直观图如图.∠PCB=90°,∠PCA=90°,∠ABC=90°.
解:(I)直观图如图.∠PCB=90°,∠PCA=90°,∠ABC=90°.
VP-ABC=
S△ABC•PC=
×
×5×
×6
=12(cm3)…(6分)
(II)互相垂直的面有:
面PAC⊥面ABC,面PBC⊥面ABC,
而PAB⊥而PBC…(8分)
证明如下:
由题意知,PC⊥面ABC,PC?面PAC,PC?面PBC,
∴面PAC⊥面ABC,而PBC⊥面ABC…(10分)
∵PC⊥面ABC,∴PC⊥AB
又∵AB⊥BC,BC∩PC=C,
∴AB⊥面PBC,
∵AB?面PAB,
∴面PAB⊥面PBC…(12分)
 解:(I)直观图如图.∠PCB=90°,∠PCA=90°,∠ABC=90°.
解:(I)直观图如图.∠PCB=90°,∠PCA=90°,∠ABC=90°.VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 12 |
| 5 |
=12(cm3)…(6分)
(II)互相垂直的面有:
面PAC⊥面ABC,面PBC⊥面ABC,
而PAB⊥而PBC…(8分)
证明如下:
由题意知,PC⊥面ABC,PC?面PAC,PC?面PBC,
∴面PAC⊥面ABC,而PBC⊥面ABC…(10分)
∵PC⊥面ABC,∴PC⊥AB
又∵AB⊥BC,BC∩PC=C,
∴AB⊥面PBC,
∵AB?面PAB,
∴面PAB⊥面PBC…(12分)
点评:本题考查直线与平面垂直的判定,几何体直观图的画法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
一几何体的三视图如图所示,则该几何体的体积是( )
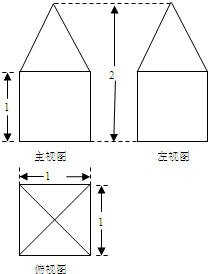

| A、2 | ||||
B、
| ||||
C、1+
| ||||
D、1+
|
 已知一几何体的三视图如图,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择5个顶点,它们可能是如下各种几何形体的5个顶点,这些几何形体是(写出所有正确结论的编号)
已知一几何体的三视图如图,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择5个顶点,它们可能是如下各种几何形体的5个顶点,这些几何形体是(写出所有正确结论的编号) 已知一几何体的三视图如图所示,则其体积为
已知一几何体的三视图如图所示,则其体积为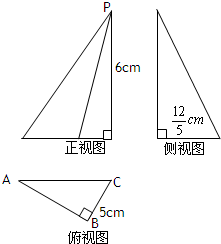 一几何体的三视图如图:
一几何体的三视图如图: (2011•开封一模)已知一几何体的三视图如图,则该几何体外接球的表面积为
(2011•开封一模)已知一几何体的三视图如图,则该几何体外接球的表面积为