题目内容
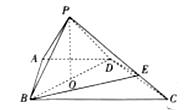
【题目】如图,在矩形ABCD中,![]() ,E为AB的中点.将
,E为AB的中点.将![]() 沿DE翻折,得到四棱锥
沿DE翻折,得到四棱锥![]() .设
.设![]() 的中点为M,在翻折过程中,有下列三个命题:
的中点为M,在翻折过程中,有下列三个命题:
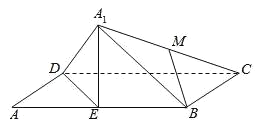
①总有![]() 平面
平面![]() ;
;
②线段BM的长为定值;
③存在某个位置,使DE与![]() 所成的角为90°.
所成的角为90°.
其中正确的命题是_______.(写出所有正确命题的序号)
【答案】①②
【解析】
取![]() D的中点N,连接MN,EN,根据四边形MNEB为平行四边形判断①,②,假设DE⊥
D的中点N,连接MN,EN,根据四边形MNEB为平行四边形判断①,②,假设DE⊥![]() C得出矛盾结论判断③.
C得出矛盾结论判断③.
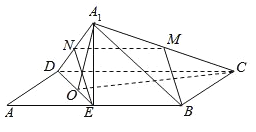
取![]() D的中点N,连接MN,EN,
D的中点N,连接MN,EN,
则MN为△![]() CD的中位线,
CD的中位线,
∴MN∥![]() CD,且MN=
CD,且MN=![]() CD
CD
又E为矩形ABCD的边AB的中点,∴BE∥![]() CD,且BE=
CD,且BE=![]() CD
CD
∴MN∥BE,且MN=BE即四边形MNEB为平行四边形,∴BM∥EN,
又EN平面A1DE,BM平面A1DE,
∴BM∥平面![]() DE,故①正确;
DE,故①正确;
由四边形MNEB为平行四边形可得BM=NE,
而在翻折过程中,NE的长度保持不变,故BM的长为定值,故②正确;
取DE的中点O,连接![]() O,CO,
O,CO,
由![]() D=
D=![]() E可知
E可知![]() O⊥DE,
O⊥DE,
若DE⊥![]() C,则DE⊥平面
C,则DE⊥平面![]() OC,
OC,
∴DE⊥OC,又∠CDO=90°﹣∠ADE=45°,
∴△OCD为等腰直角三角形,故而CD![]() OD,
OD,
而OD![]() DE
DE![]() ,CD=4,与CD
,CD=4,与CD![]() OD矛盾,故DE与
OD矛盾,故DE与![]() C所成的角不可能为90°.
C所成的角不可能为90°.
故③错误.
故答案为:①②.

 阅读快车系列答案
阅读快车系列答案【题目】随着移动互联网的发展,与餐饮美食相关的手机![]() 软件层出不穷.为调查某款订餐软件的商家的服务情况,统计了10次订餐“送达时间”,得到茎叶图如下:(时间:分钟)
软件层出不穷.为调查某款订餐软件的商家的服务情况,统计了10次订餐“送达时间”,得到茎叶图如下:(时间:分钟)
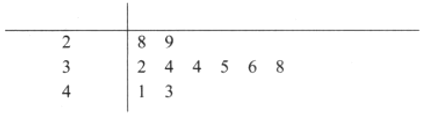
(1)请计算“送达时间”的平均数与方差:
(2)根据茎叶图填写下表:
送达时间 | 35分组以内(包括35分钟) | 超过35分钟 |
频数 | A | B |
频率 | C | D |
在答题卡上写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(3)在(2)的情况下,以频率代替概率.现有3个客户应用此软件订餐,求出在35分钟以内(包括35分钟)收到餐品的人数![]() 的分布列,并求出数学期望.
的分布列,并求出数学期望.
【题目】随着社会的进步与发展,中国的网民数量急剧增加.下表是中国从![]() 年网民人数及互联网普及率、手机网民人数(单位:亿)及手机网民普及率的相关数据.
年网民人数及互联网普及率、手机网民人数(单位:亿)及手机网民普及率的相关数据.
年份 | 网民人数 | 互联网普及率 | 手机网民人数 | 手机网民普及率 |
2009 |
|
|
|
|
2010 |
|
|
|
|
2011 |
|
|
|
|
2012 |
|
|
|
|
2013 |
|
|
|
|
2014 |
|
|
|
|
2015 |
|
|
|
|
2016 |
|
|
|
|
2017 |
|
|
|
|
2018 |
|
|
|
|
(互联网普及率![]() (网民人数/人口总数)×100%;手机网民普及率
(网民人数/人口总数)×100%;手机网民普及率![]() (手机网民人数/人口总数)×100%)
(手机网民人数/人口总数)×100%)
(Ⅰ)从![]() 这十年中随机选取一年,求该年手机网民人数占网民总人数比值超过80%的概率;
这十年中随机选取一年,求该年手机网民人数占网民总人数比值超过80%的概率;
(Ⅱ)分别从网民人数超过6亿的年份中任选两年,记![]() 为手机网民普及率超过50%的年数,求
为手机网民普及率超过50%的年数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)若记![]() 年中国网民人数的方差为
年中国网民人数的方差为,手机网民人数的方差为
![]() ,试判断
,试判断![]() 与
与![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)