题目内容
13.已知点P(x,y)在圆x2+y2=1上,则$\sqrt{(x-1)^{2}+(y-1)^{2}}$的最大值为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 1 | D. | $\sqrt{2}$+1 |
分析 $\sqrt{(x-1)^{2}+(y-1)^{2}}$表示点(x,y)与点(1,1)的距离,利用两点间的距离公式,即可求出$\sqrt{(x-1)^{2}+(y-1)^{2}}$的最大值.
解答 解:$\sqrt{(x-1)^{2}+(y-1)^{2}}$表示点(x,y)与点(1,1)的距离,
∵点P(x,y)在圆x2+y2=1上,
∴$\sqrt{(x-1)^{2}+(y-1)^{2}}$的最大值为$\sqrt{1+1}$+1=$\sqrt{2}$+1,
故选:D.
点评 本题考查点与圆的位置关系,考查两点间的距离公式,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
4.某里弄所有的263户家庭人口数分组表示如下:
计算总体均值μ,中位数m,方差s2和标准差s.
| 家庭人口数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 家庭数 | 20 | 29 | 48 | 50 | 46 | 36 | 19 | 8 | 4 | 3 |
2.设M和P是两个非空集合,定义M与P的差集为M-P={x|x∈M,且x∉P},则M-(M-P)=( )
| A. | P | B. | M∩P | C. | M∪P | D. | M |
11.执行如图所示的程序框图,若输出b=3,则输入的实数a的取值范围是( )
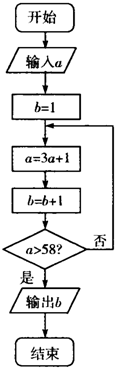

| A. | (19,+∞) | B. | (8,19] | C. | (6,19] | D. | ($\frac{5}{3}$,6] |