题目内容
【题目】已知函数![]() (
(![]() 且
且![]() )是定义在
)是定义在![]() 上的奇函数.
上的奇函数.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)判断并用定义证明![]() 的单调性;
的单调性;
(Ⅲ)若![]() ,且
,且![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;
;
(Ⅱ)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减;证明见解析;
上单调递减;证明见解析;
(Ⅲ)![]() .
.
【解析】
(Ⅰ)由题意![]() ,由奇函数的特征得
,由奇函数的特征得![]() ,利用对数的运算性质求实数
,利用对数的运算性质求实数![]() 的值;
的值;
(Ⅱ)设![]() ,且
,且![]() ,利用作差法用定义证明
,利用作差法用定义证明![]() 的单调性;
的单调性;
(Ⅲ)由![]() 可得
可得![]() 的范围,得函数
的范围,得函数![]() 的单调性,由
的单调性,由![]() 利用奇偶性得
利用奇偶性得![]() ,再根据单调性求实数
,再根据单调性求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)由题意![]() ,
,
∵函数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ;
;
(Ⅱ)由(Ⅰ)知![]() ,
,
设![]() ,且
,且![]() ,
,
则![]()
![]()
![]() ,
,
∵![]() ,∴
,∴![]()
![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∴当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
综上:当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
(Ⅲ)由![]() 得
得 ,
,
∴![]() ,由(Ⅱ)知,
,由(Ⅱ)知,![]() 在
在![]() 上单调递减,
上单调递减,
由![]() 利用奇偶性得
利用奇偶性得![]() ,
,
∴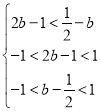 ,解得
,解得![]() ,
,
综上:实数![]() 的取值范围是
的取值范围是![]() .
.

 考前必练系列答案
考前必练系列答案【题目】某城市理论预测2020年到2024年人口总数与年份的关系如下表所示:
年份202x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请在右面的坐标系中画出上表数据的散点图;
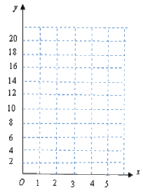
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)据此估计2025年该城市人口总数.
(参考公式: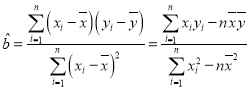 ,
,![]() )
)
【题目】社会上有人认为在机动车驾驶技术上,男性优于女性,这是真的么?某社会调查机构与交警合作随机统计了经常开车的100名驾驶员最近三个月内是否有交通事故或交通违法事件发生,得到下面的列联表:
男 | 女 | 总计 | |
无 | 40 | 35 | 75 |
有 | 15 | 10 | 25 |
总计 | 55 | 45 | 100 |
附: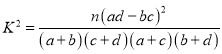
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
据此表,可得( ).
A.认为机动车驾驶技术与性别有关的可靠性不足![]()
B.认为机动车驾驶技术与性别有关的可靠性超过![]()
C.认为机动车驾驶技术与性别有关的可靠性超过![]()
D.认为机动车驾驶技术与性别有关的可靠性超过![]()
