题目内容
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关心的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 |
|
|
|
|
|
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 |
|
|
|
|
|
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在![]() ,
,![]() 的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
的被调查者中赞成“延迟退休”的人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在![]() 的被调查者中选取的2人都赞成“延迟退休”的概率;
的被调查者中选取的2人都赞成“延迟退休”的概率;
(Ⅱ)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(Ⅰ)![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】试题分析:(1)利用古典概型的概率公式,求出年龄在![]() 的被调查者中选取的2人都是赞成的概率;
的被调查者中选取的2人都是赞成的概率;
(2)由已知得![]() 的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量
的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
试题解析:
(Ⅰ)设“年龄在![]() 的被调查者中选取的2人都是赞成”为事件
的被调查者中选取的2人都是赞成”为事件![]() ,
,
所以![]()
(Ⅱ)![]() 的可能取值为0,1,2,3
的可能取值为0,1,2,3
所以![]() ,
,![]()
![]() ,
,![]()
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.

练习册系列答案
相关题目
【题目】网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):
年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
销售收入y | 16 | 23 | 25 | 26 | 30 |
(1)求y关于x的回归方程; (2)2017年度该电商准备投入广告费1.5亿元,
利用(1)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 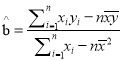
![]() ,选用数据:
,选用数据: ![]() ,
, ![]()
