题目内容
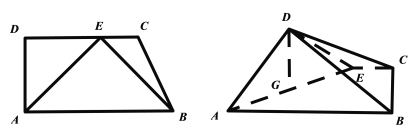
【题目】如图,矩形ABCD中,AD=2AB=4,E为BC的中点,现将△BAE与△DCE折起,使得平面BAE及平面DEC都与平面ADE垂直.

(1)求证:BC∥平面ADE;
(2)求二面角A﹣BE﹣C的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)过点B作BM⊥AE于M,过点C作CN⊥ED于N,连接MN,证明BC∥MN即可;
(2)以E为原点,ED为x轴,EA为y轴,建立空间直角坐标系Exyz,求出平面CEB的法向量![]() ,平面AEB的法向量
,平面AEB的法向量![]() ,计算
,计算![]() 即可.
即可.
(1)过点B作BM⊥AE,垂足为M,过点C作CN⊥ED于N,连接MN,如图所示;
∵平面BAE⊥平面ADE,平面DCE⊥平面ADE,
∴BM⊥平面ADE,CN⊥ADE,
∴BM∥CN;
由题意知Rt△ABE≌Rt△DCE,
∴BM=CN,
∴四边形BCNM是平行四边形,
∴BC∥MN;
又BC平面ADE,MN平面ADE,
∴BC∥平面ADE;
(2)由已知,AE、DE互相垂直,以E为原点,ED为x轴,EA为y轴,建立空间直角坐标系Exyz,如图所示;
则E(0,0,0),B(0,![]() ,
,![]() ),C(
),C(![]() ,0,
,0,![]() ),
),![]() ,
,
设平面CEB的法向量为![]() =(x,y,z),
=(x,y,z),
则 ,
,
即 ,
,
令y=1,则z=1,x=1,
∴![]() =(1,1,1);
=(1,1,1);
设平面AEB的法向量为![]() =(x,y,z),
=(x,y,z),
则 ,易求得
,易求得![]() =(1,0,0),
=(1,0,0),
又 ,
,
二面角ABEC的平面角的余弦值为![]() .
.

【题目】根据《山东省全民健身实施计划(2016-2020年)》,到2020年乡镇(街道)普遍建有“两个一”工程,即一个全民健身活动中心或灯光篮球场、一个多功能运动场.某市把甲、乙、丙、丁四个多功能运动场全部免费为市民开放.

(1)在一次全民健身活动中,四个多功能运动场的使用场数如图,用分层抽样的方法从甲、乙、丙、丁四场馆的使用场数中依次抽取![]() ,
,![]() ,
,![]() ,
,![]() 共25场,在
共25场,在![]() ,
,![]() ,
,![]() ,
,![]() 中随机取两数,求这两数和
中随机取两数,求这两数和![]() 的分布列和数学期望;
的分布列和数学期望;
(2)设四个多功能运动场一个月内各场使用次数之和为![]() ,其相应维修费用为
,其相应维修费用为![]() 元,根据统计,得到如下表的
元,根据统计,得到如下表的![]() 与
与![]() 数据:
数据:
| 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 2302 | 2708 | 2996 | 3219 | 3401 | 3555 | 3689 |
| 2.49 | 2.99 | 3.55 | 4.00 | 4.49 | 4.99 | 5.49 |
(i)用最小二乘法求![]() 与
与![]() 之间的回归直线方程;
之间的回归直线方程;
(ii)![]() 叫做运动场月惠值,根据(i)的结论,试估计这四个多功能运动场月惠值最大时
叫做运动场月惠值,根据(i)的结论,试估计这四个多功能运动场月惠值最大时![]() 的值.
的值.
参考数据和公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
 ,
,![]() .
.