题目内容
【题目】选修4-4:坐标系与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, ![]() 点的极坐标为
点的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() :
: ![]() 的距离的最小值.
的距离的最小值.
【答案】(1)点![]()
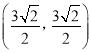 ;
; 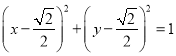 (2)
(2)![]()
【解析】试题分析:(1)由![]() 的极坐标为
的极坐标为![]() ,利用
,利用![]() 可得
可得![]() 点的直角坐标,曲线
点的直角坐标,曲线![]() 的参数方程展开可得:
的参数方程展开可得: ![]() ,利用
,利用![]() 以及
以及![]() 可得出直角坐标方程;(2)直线
可得出直角坐标方程;(2)直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,设
,设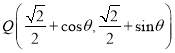 ,则
,则![]() ,利用点到直线的距离公式与三角函数的单调性值域即可得出.
,利用点到直线的距离公式与三角函数的单调性值域即可得出.
试题解析:(1)点![]() 的直角坐标为
的直角坐标为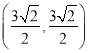 ;
;
由![]() 得
得![]() ①
①
将![]() ,
, ![]() ,
, ![]() 代入①,
代入①,
可得曲线![]() 的直角坐标方程为
的直角坐标方程为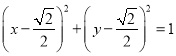 .
.
(2)直线![]()
![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
设点![]() 的直角坐标为
的直角坐标为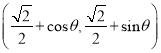 ,则
,则![]() ,
,
那么![]() 到直线
到直线![]() 的距离:
的距离:
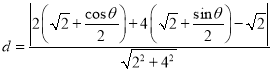
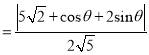
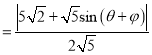 ,
,
![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
所以![]() 到直线
到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目