题目内容
用描述法表示被5除余1的正整数集合： ．
考点：集合的表示法
专题：集合
分析：被5除余1，也就是该数能写成5n+1，n∈N的形式，然后借助于集合的描述法表示即可．
解答：解：据题，设该数为x，
则该数x满足
x=5n+1，n∈N，
∴所求的正整数集合为{x|x=5n+1，n∈N}
故答案为：{x|x=5n+1，n∈N}
则该数x满足
x=5n+1，n∈N，
∴所求的正整数集合为{x|x=5n+1，n∈N}
故答案为：{x|x=5n+1，n∈N}
点评：本题考查集合的描述法表示方法，结合整除问题求解，属于基础题，难度小．
练习册系列答案
相关题目
下列集合中，不是方程（x+1）（x-2）（x-3）=0的解集的集合是（ ）
| A、{-1，2，3} | B、{3，-1，2} | C、{x|（x+1）（x-2）（x-3）=0} | D、{（-1，2，3）} |
设集合A={x|x2-3x-2＜0}，B={x|2＜2x＜8}，则（ ）
| A、A=B | B、A?B | C、A⊆B | D、A∩B=∅ |
若集合A={x|x2=1}，B={x|x2-3x+2=0}，则集合A∪B=（ ）
| A、{1} | B、{1，2} | C、{-1，1，2} | D、{-1，1，-2} |
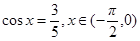，则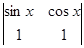
=_______