题目内容
集合C={y|y=-x2+2x+3，x∈R，y∈N}用列举法表示是 ．
考点：集合的表示法
专题：集合
分析：首先，集合C的构成元素为函数值y=-x2+2x+3，x∈R，y∈N，可以先求解函数的值域，然后，借助于x∈R，y∈N进行选择即可．
解答：解：∵y=-x2+2x+3=-（x-1）2+4，
∴y≤4，
∵y∈N，
∴y=0，1，2，3，4，
∴集合C={0，1，2，3，4}，
故答案为{0，1，2，3，4}．
∴y≤4，
∵y∈N，
∴y=0，1，2，3，4，
∴集合C={0，1，2，3，4}，
故答案为{0，1，2，3，4}．
点评：本题重点考查函数的值域、集合的列举法表示等知识，属于基础题．
练习册系列答案
相关题目
设集合N={x|x2≤x}，则N=（ ）
| A、{0，1} | B、[0，1] | C、（0，1） | D、[0，1） |
已知M={a||a|≥2}，A={a|（a-2）（a2-3）=0，a∈M}则集合A的子集共有（ ）
| A、1个 | B、2个 | C、4个 | D、8 个 |
设集合A是N*的某个有限子集，集合S={（a，b）|a∈A，b∈A，a+b∈A}，集合T={（a，b）|a∈A，b∈A，a-b∈A}．则下列说法中正确的是（其中|M|表示集合M中元素个数）（ ）
| A、|S|＞|T| | B、|S|=|T| | C、|S|＜|T| | D、不能确定 |
=
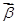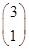，变换T的矩阵为A=
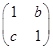，平面上的点P（1，1）在变换T作用下得到点P′（3，3），求A-1