题目内容
被4除余数为1的所有自然数组成的集合是 ．
考点：集合的表示法
专题：计算题,集合
分析：被4除余数为1的所有自然数为x=4n+1，n∈N*，即可得出结论．
解答：解：被4除余数为1的所有自然数为x=4n+1，n∈N*，
∴被4除余数为1的所有自然数组成的集合是{x|x=4n+1，n∈N*}．
故答案为：{x|x=4n+1，n∈N*}．
∴被4除余数为1的所有自然数组成的集合是{x|x=4n+1，n∈N*}．
故答案为：{x|x=4n+1，n∈N*}．
点评：本题考查集合的表示方法，考查描述法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
集合{x∈N|-1≤x＜5}用列举法表示为（ ）
| A、{0，1，2，3，4} | B、{-1，0，1，2，3，4} | C、{1，2，3，4} | D、{1，2，3，4，5} |
已知集合M={a，b，c}，N={b，c，d}，则（ ）
| A、M⊆N | B、N⊆M | C、M∩N={b，c} | D、M∪N={a，d} |
设集合A={x|-1＜x＜1}，B={x|log2x≤0}，则A∪B=（ ）
| A、{x|-1＜x＜1} | B、{x|0＜x＜1} | C、{x|-1＜x≤1} | D、{x|-∞＜x≤1} |
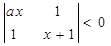对任意
恒成立，则实数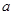
的取值范围是 ．