题目内容
【题目】函数f（x）=ax2+bx（a＞0，b＞0）在点（1，f（1））处的切线斜率为2，则 
的最小值是（ ）
A.10
B.9
C.8
D.
【答案】B
【解析】解：由f（x）=ax2+bx，得f′（x）=2ax+b， 又f（x）=ax2+bx（a＞0，b＞0）在点（1，f（1））处的切线斜率为2，
所以f′（1）=2a+b=2，即 
．
则 
= 
．
当且仅当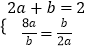 
，即 
时“=”成立．
所以 的最小值是9．
故选B．
【考点精析】本题主要考查了基本求导法则和基本不等式的相关知识点，需要掌握若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导；基本不等式：
,（当且仅当
时取到等号）；变形公式：
才能正确解答此题．
练习册系列答案
相关题目
【题目】下列四个命题中错误的是（ ）
A.在一次试卷分析中，从每个考室中抽取第5号考生的成绩进行统计，不是简单随机抽样
B.对一个样本容量为100的数据分组，各组的频数如下：
区间 | [17，19） | [19，21） | [21，23） | [23，25） | [25，27） | [27，29） | [29，31） | [31，33] |
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的58%
C.设产品产量与产品质量之间的线性相关系数为﹣0.91，这说明二者存在着高度相关
D.通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如表列联表：
男 | 女 | 总计 | |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 
，则有99%以上的把握认为“选择过马路方式与性别有关”
