题目内容
已知椭圆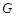 的离心率为
的离心率为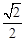 ,短轴端点分别为
,短轴端点分别为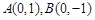 .
.
(1)求椭圆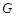 的标准方程;
的标准方程;
(2)若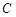 ,
,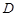 是椭圆
是椭圆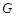 上关于
上关于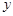 轴对称的两个不同点,直线
轴对称的两个不同点,直线 与
与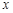 轴交于点
轴交于点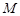 ,判断以线段
,判断以线段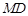 为直径的圆是否过点
为直径的圆是否过点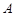 ,并说明理由.
,并说明理由.
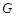 的离心率为
的离心率为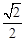 ,短轴端点分别为
,短轴端点分别为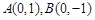 .
.(1)求椭圆
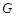 的标准方程;
的标准方程;(2)若
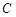 ,
,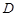 是椭圆
是椭圆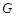 上关于
上关于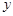 轴对称的两个不同点,直线
轴对称的两个不同点,直线 与
与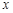 轴交于点
轴交于点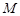 ,判断以线段
,判断以线段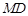 为直径的圆是否过点
为直径的圆是否过点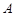 ,并说明理由.
,并说明理由.(1)椭圆的标准方程为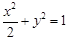 ;(2)点
;(2)点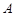 不在以线段
不在以线段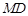 为直径的圆上.
为直径的圆上.
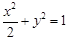 ;(2)点
;(2)点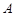 不在以线段
不在以线段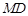 为直径的圆上.
为直径的圆上.试题分析:(1)求椭圆
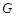 的标准方程,已知椭圆
的标准方程,已知椭圆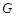 的离心率为
的离心率为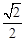 ,短轴端点分别为
,短轴端点分别为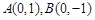 ,可设椭圆方程为
,可设椭圆方程为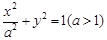 ,由
,由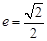 ,可得
,可得 ,从而得椭圆
,从而得椭圆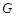 的标准方程;(2)由于
的标准方程;(2)由于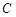 ,
,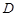 是椭圆
是椭圆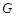 上关于
上关于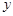 轴对称的两个不同点,可设
轴对称的两个不同点,可设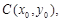 则
则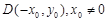 ,若点
,若点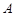 在以线段
在以线段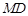 为直径的圆上,则
为直径的圆上,则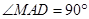 ,即
,即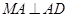 ,即
,即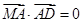 ,因此可写出直线
,因此可写出直线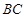 的方程为
的方程为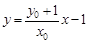 ,令
,令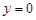 ,得
,得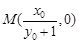 ,写出向量
,写出向量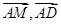 的坐标,看
的坐标,看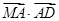 是否等于0,即可判断出.
是否等于0,即可判断出.(1)由已知可设椭圆
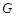 的方程为:
的方程为: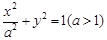 1分
1分由
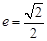 ,可得
,可得 , 3分
, 3分解得
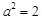 , 4分
, 4分所以椭圆的标准方程为
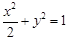 . 5分
. 5分(2)法一:设
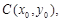 则
则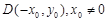 6分
6分因为
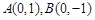 ,
,所以直线
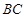 的方程为
的方程为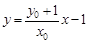 , 7分
, 7分令
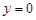 ,得
,得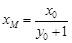 ,所以
,所以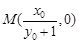 . 8分
. 8分所以
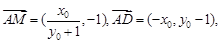 9分
9分所以
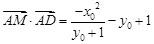 , 10分
, 10分又因为
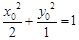 ,代入得
,代入得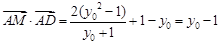 11分
11分因为
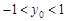 ,所以
,所以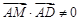 . 12分
. 12分所以
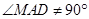 , 13分
, 13分所以点
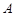 不在以线段
不在以线段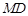 为直径的圆上. 14分
为直径的圆上. 14分法二:设直线
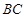 的方程为
的方程为 ,则
,则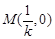 . 6分
. 6分由
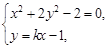 化简得到
化简得到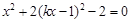 ,
,所以
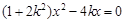 ,所以
,所以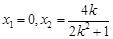 , 8分
, 8分所以
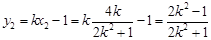 ,
,所以
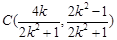 ,所以
,所以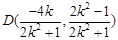 9分
9分所以
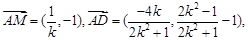 10分
10分所以
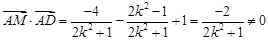 , 12分
, 12分所以
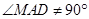 , 13分
, 13分所以点
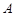 不在以线段
不在以线段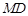 为直径的圆上. 14分
为直径的圆上. 14分
练习册系列答案
相关题目
 ,过点
,过点 任作一直线与
任作一直线与 相交于
相交于 两点,过点
两点,过点 作
作 轴的平行线与直线
轴的平行线与直线 相交于点
相交于点 (
( 为坐标原点).
为坐标原点).
 (不含
(不含 轴)与直线
轴)与直线 相交于点
相交于点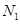 ,与(1)中的定直线相交于点
,与(1)中的定直线相交于点 ,证明:
,证明: 为定值,并求此定值.
为定值,并求此定值. 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为 的直线和曲线
的直线和曲线 ,过
,过 的直线与曲线
的直线与曲线 ,过
,过 的直线与曲线
的直线与曲线 ,如此下去,一般地,过点
,如此下去,一般地,过点 作斜率为
作斜率为 的直线与曲线
的直线与曲线 ,设点
,设点 (
( ).
). ,并求
,并求 与
与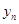 的关系式(
的关系式( (
( ,向哪一点无限接近?说明理由;
,向哪一点无限接近?说明理由; ,数列
,数列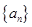 的前
的前 项和为
项和为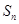 ,试比较
,试比较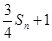 与
与 的大小,并证明你的结论.
的大小,并证明你的结论. 的焦点为
的焦点为 ,点
,点 ,线段
,线段 的中点在抛物线上. 设动直线
的中点在抛物线上. 设动直线 与抛物线相切于点
与抛物线相切于点 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以 为直径的圆记为圆
为直径的圆记为圆 .
. 的值;
的值; 轴必有公共点;
轴必有公共点;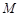 ,使得圆
,使得圆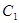 的圆心在坐标原点
的圆心在坐标原点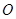 ,且恰好与直线
,且恰好与直线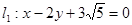 相切,设点A为圆上一动点,
相切,设点A为圆上一动点,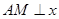 轴于点
轴于点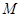 ,且动点
,且动点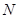 满足
满足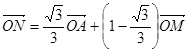 ,设动点
,设动点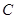
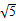 ,+∞)
,+∞)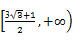
 .
. =1(a>0,b>0)的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足|
=1(a>0,b>0)的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足| |=3|
|=3| |,则此双曲线的渐近线方程为________.
|,则此双曲线的渐近线方程为________.


