题目内容
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为 .
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由.
 .
.(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由.
(1)x2=2y (2)存在,M(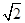 ,1)
,1)
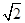 ,1)
,1)(1)依题意知F(0, ),圆心Q在线段OF的垂直平分线y=
),圆心Q在线段OF的垂直平分线y= 上,
上,
因为抛物线C的准线方程为y=- ,
,
所以 =
= ,即p=1.
,即p=1.
因此抛物线C的方程为x2=2y.
(2)假设存在点M(x0, )(x0>0)满足条件,抛物线C在点M处的切线斜率为y′|x=x0=(
)(x0>0)满足条件,抛物线C在点M处的切线斜率为y′|x=x0=( )′|x=x0=x0,
)′|x=x0=x0,
所以直线MQ的方程为y- =x0(x-x0).
=x0(x-x0).
令y= 得xQ=
得xQ= +
+ ,
,
所以Q( +
+ ,
, ).
).
又|QM|=|OQ|,
故( -
- )2+(
)2+( -
- )2=(
)2=( +
+ )2+
)2+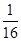 ,
,
因此( -
- )2=
)2= .
.
又x0>0,所以x0=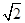 ,此时M(
,此时M(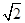 ,1).
,1).
故存在点M(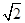 ,1),使得直线MQ与抛物线C相切于点M.
,1),使得直线MQ与抛物线C相切于点M.
 ),圆心Q在线段OF的垂直平分线y=
),圆心Q在线段OF的垂直平分线y= 上,
上,因为抛物线C的准线方程为y=-
 ,
,所以
 =
= ,即p=1.
,即p=1.因此抛物线C的方程为x2=2y.
(2)假设存在点M(x0,
 )(x0>0)满足条件,抛物线C在点M处的切线斜率为y′|x=x0=(
)(x0>0)满足条件,抛物线C在点M处的切线斜率为y′|x=x0=( )′|x=x0=x0,
)′|x=x0=x0,所以直线MQ的方程为y-
 =x0(x-x0).
=x0(x-x0).令y=
 得xQ=
得xQ= +
+ ,
,所以Q(
 +
+ ,
, ).
).又|QM|=|OQ|,
故(
 -
- )2+(
)2+( -
- )2=(
)2=( +
+ )2+
)2+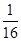 ,
,因此(
 -
- )2=
)2= .
.又x0>0,所以x0=
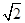 ,此时M(
,此时M(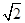 ,1).
,1).故存在点M(
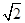 ,1),使得直线MQ与抛物线C相切于点M.
,1),使得直线MQ与抛物线C相切于点M.
练习册系列答案
相关题目
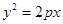 (
(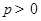 )的准线与
)的准线与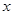 轴交于点
轴交于点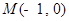 .
.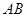 (直线与抛物线交于点
(直线与抛物线交于点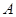 ,
,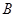 ),使得三角形
),使得三角形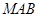 的面积
的面积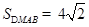 ?若存在,请求出直线
?若存在,请求出直线 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+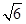 =0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
=0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点. ·
· 的取值范围;
的取值范围; a2.
a2.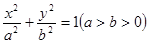 的右焦点为
的右焦点为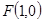 ,离心率
,离心率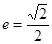 ,
,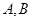 是椭圆上的动点.
是椭圆上的动点.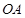 与
与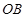 的斜率乘积
的斜率乘积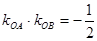 ,动点
,动点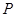 满足
满足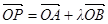 ,(其中实数
,(其中实数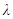 为常数).问是否存在两个定点
为常数).问是否存在两个定点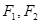 ,使得
,使得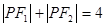 ?若存在,求
?若存在,求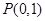 与抛物线
与抛物线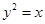 有且只有一个交点的直线有( )
有且只有一个交点的直线有( )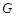 的离心率为
的离心率为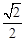 ,短轴端点分别为
,短轴端点分别为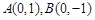 .
.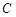 ,
,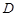 是椭圆
是椭圆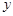 轴对称的两个不同点,直线
轴对称的两个不同点,直线 与
与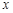 轴交于点
轴交于点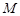 ,判断以线段
,判断以线段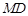 为直径的圆是否过点
为直径的圆是否过点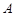 ,并说明理由.
,并说明理由. 、
、 为椭圆
为椭圆 的左右焦点,点
的左右焦点,点 为其上一点,且有
为其上一点,且有
 .
. 的标准方程;
的标准方程; 与椭圆
与椭圆 交于
交于 、
、 两点,过
两点,过 与椭圆
与椭圆 两点,求四边形
两点,求四边形 的面积
的面积 的最大值.
的最大值. 的焦点为F,过F作直线交抛物线于A、B两点,设
的焦点为F,过F作直线交抛物线于A、B两点,设 则
则 ( )
( ) D.1
D.1