题目内容
【题目】如图，已知⊙O是△ABC的外接圆，AB=BC，AD是BC边上的高，AE是⊙O的直径．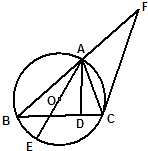 
（1）求证：ACBC=ADAE；
（2）过点C作⊙O的切线交BA的延长线于点F，若AF=3，CF=9，求AC的长．
【答案】
（1）证明：如图所示，连接BE
∵AE是⊙O的直径，∴∠ABE=90°．
又∠E=∠ACB．
∵AD⊥BC，∠ADC=90°．
∴△ABE∽△ADC，∴ 
，∴ABAC=ADAE．
又AB=BC，∴BCAC=ADAE．
（2）解：∵CF是⊙O的切线，∴CF2=AFBF，
∵AF=3，CF=9，∴92=3BF，解得BF=27．
∴AB=BF﹣AF=24．
∵∠ACF=∠FBC，∠CFB=∠AFC，∴△AFC∽△CFB，
∴ 
= 
，∴AC= 
=8．
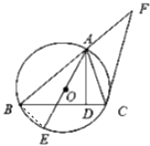
【解析】（1）如图所示，连接BE．由于AE是⊙O的直径，可得∠ABE=90°．利用∠E=∠ACB．进而得到△ABE∽△ADC，即可得到．（2）利用切割线定理可得CF2=AFBF，可得BF．再利用△AFC∽△CFB，可得 = ，即可得出．
练习册系列答案
相关题目
