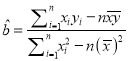题目内容
【题目】在![]() 中,内角A,B,C的对边分别是a,b,c,且a2+b2+
中,内角A,B,C的对边分别是a,b,c,且a2+b2+![]() ab=c2.
ab=c2.
(1)求C;
(2)设cos Acos B=![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)1或4.
;(2)1或4.
【解析】(1)因为a2+b2+![]() ab=c2,
ab=c2,
所以由余弦定理有cos C=![]() ,
,
故![]() .
.
(2)由题意得![]() =
=![]() ,
,
因此(tan αsin Acos A)(tan αsin Bcos B)=![]() ,
,
即tan2αsin Asin Btan α(sin Acos B+cos Asin B)+cos Acos B=![]() ,
,
即tan2αsin Asin Btan αsin(A+B)+cos Acos B=![]() ①.
①.
因为![]() ,
,
所以A+B=![]() ,
,
所以sin(A+B)=![]() .
.
因为cos(A+B)=cos Acos Bsin Asin B,即![]() -sin Asin B=
-sin Asin B=![]() ,
,
则sin Asin B=![]() .
.
代入①得tan2α5tan α+4=0,解得tan α=1或tan α=4.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
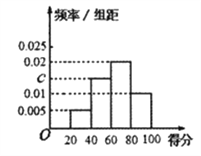
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校安全教育活动的成效.若
的方差)来评估该校安全教育活动的成效.若![]() ,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?