题目内容
19.已知A、B、C是锐角三角形的内角.$\sqrt{3}$sinA和(-cosA)是方程x2-x+2a=0的两根.(1)求角A;
(2)若$\frac{1+2sinBcosB}{co{s}^{2}B-si{n}^{2}B}$=-3,求tanB.
分析 (1)根据题意,利用韦达定理列出关系式,利用两角和与差的正弦函数公式化简,利用特殊角的三角函数值即可求出A的度数;
(2)已知等式分子利用完全平方公式化简,分母利用平方差公式化简,约分后分子分母除以cosB,利用同角三角函数间基本关系化简,整理即可求出tanB的值.
解答 解:(1)∵$\sqrt{3}$sinA和(-cosA)是方程x2-x+2a=0的两根,
∴$\sqrt{3}$sinA-cosA=1,即2sin(A-$\frac{π}{6}$)=1,
∴sin(A-$\frac{π}{6}$)=$\frac{1}{2}$,
∵A为锐角,
∴A=$\frac{π}{3}$;
(2)已知等式变形得:$\frac{(sinB+cosB)^{2}}{(cosB+sinB)(cosB-sinB)}$=3,即$\frac{sinB+cosB}{cosB-sinB}$=3,
分子分母除以cosB得:$\frac{tanB+1}{1-tanB}$=3,
整理得:tanB=$\frac{1}{2}$.
点评 此题考查了同角三角函数间基本关系的运用,韦达定理,以及两角和与差的正弦函数公式,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
10.求tan570°的值为( )
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
4.已知P为圆x2+y2=9上的任意一点,EF为圆N:(x-1)2+y2=1的任意一条直径,则$\overrightarrow{PE}•\overrightarrow{PF}$的取值范围( )
| A. | [-1,15] | B. | [-1,9] | C. | [3,15] | D. | [0,9] |
3.过曲线S:y=3x-x3上一点A(2,-2)的切线方程为( )
| A. | y=-2 | B. | 9x+y-16=0 | C. | 9x+y-16=0或y=-2 | D. | 9x-y-16=0 |
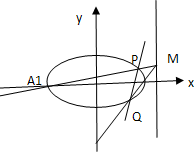 已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆上的点到焦点的距离的最小值为2-$\sqrt{3}$,其离心率e是方程2x2-3$\sqrt{3}$x+3=0的根.
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆上的点到焦点的距离的最小值为2-$\sqrt{3}$,其离心率e是方程2x2-3$\sqrt{3}$x+3=0的根.