题目内容
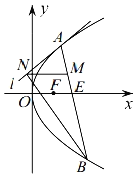
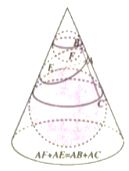
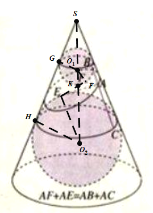
【题目】如图所示，在顶角为
圆锥内有一截面，在圆锥内放半径分别为
的两个球与圆锥的侧面、截面相切，两个球分别与截面相切于
，则截面所表示的椭圆的离心率为( )
（注：在截口曲线上任取一点
，过作圆锥的母线，分别与两个球相切于点
，由相切的几何性质可知，
，
，于是
，为椭圆的几何意义）
A.
B.
C.
D.
【答案】C
【解析】
设两球的球心分别为
，
，圆锥顶点为
，取两球与圆锥同一母线上的切点
，
，
连接
，
，
，
，连接
交
于
，由题意可得
，再利用平面几何知识即可得
，即可得解.
设两球的球心分别为，，圆锥顶点为，取两球与圆锥同一母线上的切点，，
连接，，，，连接交于，
由顶角为
，两个球的半径分别为
，
，
可知
，
，
，
，
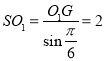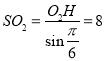所以
即
，
，
由
可得
，
所以
，所以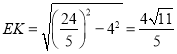
，
，
所以该椭圆离心率
.
故选：C.
练习册系列答案
相关题目
