题目内容
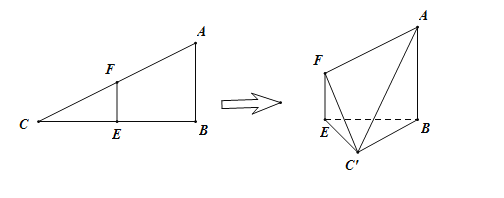
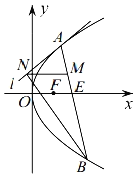
【题目】如图，已知点
，
，抛物线
的焦点
为线段
中点.
（1）求抛物线
的方程；
（2）过点
的直线交抛物线于
两点，
，过点
作抛物线的切线
，
为切线上的点，且
轴，求
面积的最小值.
【答案】（1）
；（2）
.
【解析】
1
由已知得焦点
，所以
，从而求出抛物线C的方程；2设
，
，
，设直线l方程为：
，与抛物线方程联立，利用
求得
，所以直线l的方程为：
，由
，求得点M的坐标，进而求出点N的坐标，所以
设直线AB的方程为：
，与抛物线方程联立，设直线l方程为：，利用韦达定理代入
，利用基本不等式即可求出
面积的最小值．
（1）由已知得焦点
的坐标为
，
，
抛物线
的方程为：；
（2）设直线
的方程为：，设，，，
联立方程
，消去
得：
，
，
，
，
设直线
方程为：，
联立方程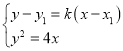
，消去得：
，
由相切得：
，
，
又
，
，
，
，
直线的方程为：，
由，得
，
，
将代入直线方程，解得
，
所以
，
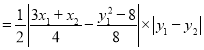
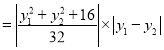
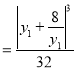又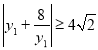
，
所以
，当且仅当
时，取到等号，
所以面积的最小值为.
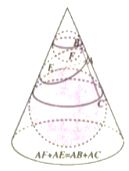
【题目】某同学使用某品牌暖水瓶，其内胆规格如图所示．若水瓶内胆壁厚不计，且内胆如图分为①②③④四个部分，它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱体．若其中圆台部分的体积为
，且水瓶灌满水后盖上瓶塞时水溢出
．记盖上瓶塞后，水瓶的最大盛水量为
，
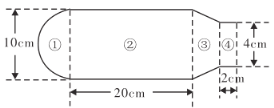
（1）求；
（2）该同学发现：该品牌暖水瓶盛不同体积的热水时，保温效果不同．为了研究保温效果最好时暖水瓶的盛水体积，做以下实验：把盛有最大盛水量的水的暖水瓶倒出不同体积的水，并记录水瓶内不同体积水在不同时刻的水温，发现水温
（单位：℃）与时刻
满足线性回归方程
，通过计算得到下表：
倒出体积 | 0 | 30 | 60 | 90 | 120 |
拟合结果 |
|
|
|
|
|
倒出体积 | 150 | 180 | 210 | … | 450 |
拟合结果 |
|
|
| … |
|
注：表中倒出体积
（单位：
）是指从最大盛水量中倒出的那部分水的体积．其中：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
令
．对于数据
，可求得回归直线为
，对于数据
，可求得回归直线为
．
（ⅰ）指出
的实际意义，并求出回归直线
的方程（参考数据：
）；
（ⅱ）若与
的交点横坐标即为最佳倒出体积，请问保温瓶约盛多少体积水时（盛水体积保留整数，且
取3.14）保温效果最佳？
附：对于一组数据
，其回归直线
中的斜率和截距的最小二乘估计分别为
．
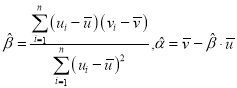【题目】某中学从甲乙两个教师所教班级的学生中随机抽取100人，每人分别对两个教师进行评分，满分均为100分，整理评分数据，将分数以10为组距分成6组：
，
，
，
，
，
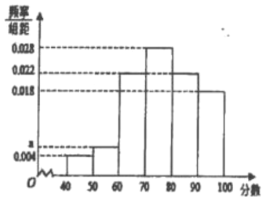
.得到甲教师的频率分布直方图，和乙教师的频数分布表：
乙教师分数频数分布表 | |
分数区间 | 频数 |
| 3 |
| 3 |
| 15 |
| 19 |
| 35 |
| 25 |
（1）在抽样的100人中，求对甲教师的评分低于70分的人数；
（2）从对乙教师的评分在
范围内的人中随机选出2人，求2人评分均在范围内的概率；
（3）如果该校以学生对老师评分的平均数是否大于80分作为衡量一个教师是否可评为该年度该校优秀教师的标准，则甲、乙两个教师中哪一个可评为年度该校优秀教师？（精确到0.1）
