题目内容
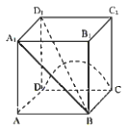
【题目】已知正方体![]() 的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
①若P为棱![]() 中点,则异面直线AP与CD所成角的正切值为
中点,则异面直线AP与CD所成角的正切值为![]() ;
;
②若P在线段![]() 上运动,则
上运动,则![]() 的最小值为
的最小值为![]() ;
;
③若P在半圆弧CD上运动,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若过点P的平面![]() 与正方体每条棱所成角相等,则
与正方体每条棱所成角相等,则![]() 截此正方体所得截面面积的最大值为
截此正方体所得截面面积的最大值为![]()
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据异面直线的夹角求解,棱锥外接球的求解,以及正方体截面的性质,对选项进行逐一分析即可.
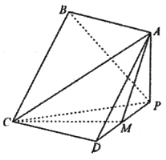
对于①,如图所示,
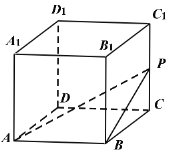
由![]() ,可知
,可知![]() 即为异面直线AE与CD所成的角.
即为异面直线AE与CD所成的角.
设正方体的棱长为2,连接BE,则在![]() 中,
中,![]() ,
,![]()
![]() ,故正确
,故正确
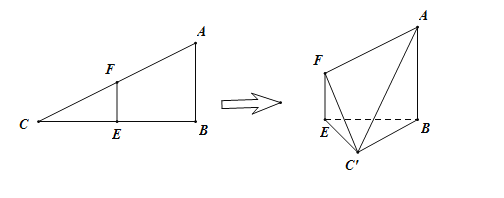
对于②,将三角形![]() 与四边形
与四边形![]() 沿
沿![]() 展开到同一个平面上,如图所示.
展开到同一个平面上,如图所示.
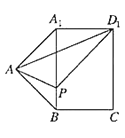
由图可知,线段![]() 的长度即为
的长度即为![]() 的最小值.
的最小值.
在![]() 中,利用余弦定理可得
中,利用余弦定理可得![]() ,故错误.
,故错误.
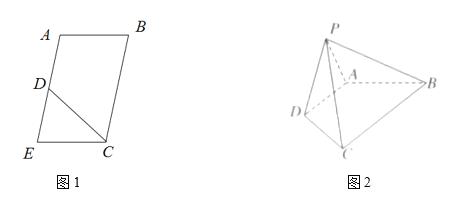
对于③,如下图所示:
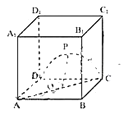
当P为![]() 中点时,三棱锥
中点时,三棱锥![]() 体积最大,
体积最大,
此时,三棱锥![]() 的外接球球心是AC中点,
的外接球球心是AC中点,
半径为![]() ﹐其表面积为
﹐其表面积为![]() .故正确.
.故正确.
对于④﹐平面![]() 与正方体的每条棱所在直线所成的角都相等,
与正方体的每条棱所在直线所成的角都相等,
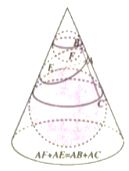
只需与过同一顶点的三条棱所成的角相等即可,如图所示:
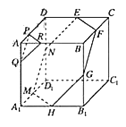
![]() .则平面PQR与正方体过点A的三条棱所成的角相等.
.则平面PQR与正方体过点A的三条棱所成的角相等.
若点E,F,G,H,M,N分别为相应棱的中点,
可得平面EFGHMN平行于平面PQR,且六边形EFGHMN为正六边形.
正方体棱长为1,所以正六边形EFGHMN的边长为![]() ,
,
可得此正六边形的面积为![]() ,为截面最大面积.
,为截面最大面积.
故正确的命题有3个.
故选:C.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某中学从甲乙两个教师所教班级的学生中随机抽取100人,每人分别对两个教师进行评分,满分均为100分,整理评分数据,将分数以10为组距分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .得到甲教师的频率分布直方图,和乙教师的频数分布表:
.得到甲教师的频率分布直方图,和乙教师的频数分布表:
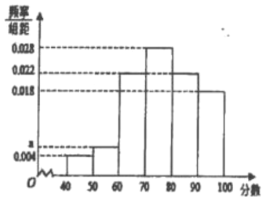
乙教师分数频数分布表 | |
分数区间 | 频数 |
| 3 |
| 3 |
| 15 |
| 19 |
| 35 |
| 25 |
(1)在抽样的100人中,求对甲教师的评分低于70分的人数;
(2)从对乙教师的评分在![]() 范围内的人中随机选出2人,求2人评分均在
范围内的人中随机选出2人,求2人评分均在![]() 范围内的概率;
范围内的概率;
(3)如果该校以学生对老师评分的平均数是否大于80分作为衡量一个教师是否可评为该年度该校优秀教师的标准,则甲、乙两个教师中哪一个可评为年度该校优秀教师?(精确到0.1)
【题目】环境问题是当今世界共同关注的问题,我国环保总局根据空气污染指数![]() 浓度,制定了空气质量标准:
浓度,制定了空气质量标准:
空气污染质量 |
|
|
|
|
|
|
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
某市政府为了打造美丽城市,节能减排,从2010年开始考查了连续六年11月份的空气污染指数,绘制了频率分布直方图,经过分析研究,决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行,即车牌尾号为单号的车辆单号出行,车牌尾号为双号的车辆双号出行(尾号为字母的,前13个视为单号,后13个视为双号).
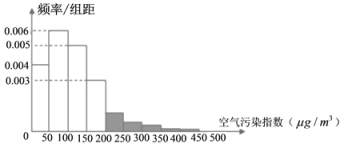
(1)某人计划11月份开车出行,求因空气污染被限号出行的概率;
(2)该市环保局为了调查汽车尾气排放对空气质量的影响,对限行三年来的11月份共90天的空气质量进行统计,其结果如表:
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 16 | 39 | 18 | 10 | 5 | 2 |
根据限行前六年180天与限行后90天的数据,计算并填写![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为空气质量的优良与汽车尾气的排放有关.
的把握认为空气质量的优良与汽车尾气的排放有关.
空气质量优良 | 空气质量污染 | 合计 | |
限行前 | |||
限行后 | |||
合计 |
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 其中
其中![]()