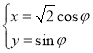题目内容
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,经过
,经过![]() 轴正半轴上点
轴正半轴上点![]() 的直线
的直线![]() 交
交![]() 于不同的两点
于不同的两点![]() 和
和![]() .
.
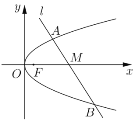
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() ,求证:原点
,求证:原点![]() 总在以线段
总在以线段![]() 为直径的圆的内部;
为直径的圆的内部;
(3)若![]() ,且直线
,且直线![]() ∥
∥![]() ,
,![]() 与
与![]() 有且只有一个公共点
有且只有一个公共点![]() ,问:△
,问:△![]() 的面积是否存在最小值?若存在,求出最小值,并求出
的面积是否存在最小值?若存在,求出最小值,并求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)存在,最小值2,
;(2)证明见解析;(3)存在,最小值2,![]() .
.
【解析】
(1)由抛物线方程以及抛物线定义,根据![]() 求出横坐标,代入
求出横坐标,代入![]() ,即可得出点的坐标;
,即可得出点的坐标;
(2)设![]() ,
,![]() ,设直线
,设直线![]() 的方程是:
的方程是:![]() ,联立直线与抛物线方程,根据韦达定理,以及向量数量积运算,得到
,联立直线与抛物线方程,根据韦达定理,以及向量数量积运算,得到![]() ,推出
,推出![]() 恒为钝角,即可得结论成立;
恒为钝角,即可得结论成立;
(3)设![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,推出直线
,推出直线![]() 的斜率
的斜率![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,代入抛物线方程,根据判别式等于零,得
,代入抛物线方程,根据判别式等于零,得![]() .设
.设![]() ,则
,则![]() ,
,![]() ,由三角形面积公式,以及基本不等式,即可求出结果.
,由三角形面积公式,以及基本不等式,即可求出结果.
(1)由抛物线方程知,焦点是![]() ,准线方程为
,准线方程为![]() ,
,
设![]() ,由
,由![]() 及抛物线定义知,
及抛物线定义知,![]() ,代入
,代入![]() 得
得![]() ,
,
所以![]() 点的坐标
点的坐标![]() 或
或![]()
(2)设![]() ,
,![]() ,
,
设直线![]() 的方程是:
的方程是:![]() ,
,
联立![]() ,消去
,消去![]() 得:
得:![]() ,由韦达定理得
,由韦达定理得 ,
,
所以![]()
![]() ,
,
故![]() 恒为钝角,
恒为钝角,
故原点![]() 总在以线段AB为直径的圆的内部.
总在以线段AB为直径的圆的内部.
(3)设![]() ,则
,则![]() ,
,
因为![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,故
,故![]() .
.
故直线![]() 的斜率
的斜率![]() .
.
因为直线![]() 和直线
和直线![]() 平行,设直线
平行,设直线![]() 的方程为
的方程为![]() ,代入抛物线方程
,代入抛物线方程
得![]() ,由题意
,由题意![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
 ,
,
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
由 得
得![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
所以![]() 点的坐标为
点的坐标为![]() ,
,![]() .
.

【题目】如图是某小区2017年1月至2018年1月当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码1—13分别对应2017年1月—2018年1月)
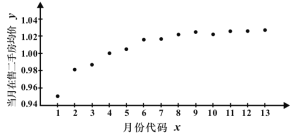
由散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程分别为
两个模型进行拟合,经过数据处理得到两个回归方程分别为![]() 和
和![]() ,并得到以下一些统计量的值:
,并得到以下一些统计量的值:
|
| |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
(1)请利用相关指数![]() 判断哪个模型的拟合效果更好;
判断哪个模型的拟合效果更好;
(2)某位购房者拟于2018年6月份购买这个小区![]() 平方米的二手房(欲
平方米的二手房(欲
购房为其家庭首套房).若购房时该小区所有住房的房产证均已满2年但未满5年,请你利用(1)中拟合效果更好的模型估算该购房者应支付的购房金额.(购房金额=房款+税费;房屋均价精确到0.001万元/平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按房屋的计税价格进行征收.(计税价格=房款),征收方式见下表:
契税 (买方缴纳) | 首套面积90平方米以内(含90平方米)为1%;首套面积90平方米以上且144平方米以内(含144平方米)为1.5%;面积144平方米以上或非首套为3% |
增值税 (卖方缴纳) | 房产证未满2年或满2年且面积在144平方米以上(不含144平方米)为5.6%;其他情况免征 |
个人所得税 (卖方缴纳) | 首套面积144平方米以内(含144平方米)为1%;面积144平方米以上或非首套均为1.5%;房产证满5年且是家庭唯一住房的免征 |
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 参考公式:相关指数
. 参考公式:相关指数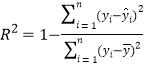 .
.
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() ,
,![]() 实验地分别用甲、乙方法培训该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.
实验地分别用甲、乙方法培训该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.
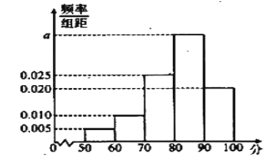
(1)求图中![]() 的值;
的值;
(2)填写下面的列联表,并判断是否有90%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: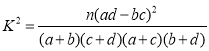 ,其中
,其中![]() .)
.)
【题目】由中央电视台综合频道![]() 和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.4.
地区当中“非常满意”的观众的概率为0.4.
非常满意 | 满意 | 合计 | |
| 35 | 10 |
|
|
|
|
|
合计 |
|
|
|
(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“非常满意”的![]() 、
、![]() 地区的人数各是多少.
地区的人数各是多少.
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附:参考公式:![]() .
.
(3)若以抽样调查的频率为概率,从![]() 、
、![]() 两个地区随机抽取2人,设抽到的观众“非常满意”的人数为
两个地区随机抽取2人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.