题目内容
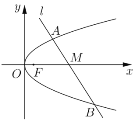
【题目】抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线上关于
是抛物线上关于![]() 轴对称的两点,点
轴对称的两点,点![]() 是抛物线准线
是抛物线准线![]() 与
与![]() 轴的交点,
轴的交点,![]() 是面积为
是面积为![]() 的直角三角形.
的直角三角形.
(1)求抛物线的方程;
(2)点![]() 在抛物线上,
在抛物线上,![]() 是直线
是直线![]() 上不同的两点,且线段
上不同的两点,且线段![]() 的中点都在抛物线上,试用
的中点都在抛物线上,试用![]() 表示
表示![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
![]() (
(![]() 或
或![]() ).
).
【解析】
(1)设出直线![]() 的方程,于抛物线联立,求出
的方程,于抛物线联立,求出![]()
![]()
![]() 的坐标,利用
的坐标,利用![]() 的面积为
的面积为![]() 列方程求出
列方程求出![]() 的值,进而可得抛物线的方程;
的值,进而可得抛物线的方程;
(2)利用![]() 是直线
是直线![]() 上不同的两点,设
上不同的两点,设![]()
![]() ,表示出
,表示出![]() 的中点坐标,代入抛物线方程,可得以
的中点坐标,代入抛物线方程,可得以![]() 为根的方程,根据判别式和韦达定理用
为根的方程,根据判别式和韦达定理用![]() 表示出
表示出![]() .
.
解:(1)不妨设点![]() 位于第一象限,
位于第一象限,
则直线![]() 的方程为
的方程为![]()
联立方程 ,解得
,解得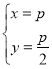
所以![]()
![]()
![]() .
.
![]() ,解得
,解得![]()
故抛物线的方程为![]()
(2)设![]()
![]()
![]()
![]() 的中点坐标为
的中点坐标为![]()
代入![]() 得:
得:![]()
![]()
同理可得:![]()
![]()
![]() 是方程
是方程![]()
![]() 的两个根
的两个根
![]()
![]()
解得![]() 或
或![]() .
.
由韦达定理可得:![]()
![]()
则![]()
![]()
![]() (
(![]() 或
或![]() )
)

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目