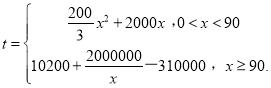题目内容
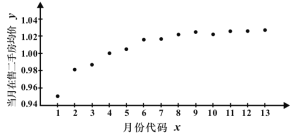
【题目】如图是某小区2017年1月至2018年1月当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码1—13分别对应2017年1月—2018年1月)
由散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程分别为
两个模型进行拟合,经过数据处理得到两个回归方程分别为![]() 和
和![]() ,并得到以下一些统计量的值:
,并得到以下一些统计量的值:
|
| |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
(1)请利用相关指数![]() 判断哪个模型的拟合效果更好;
判断哪个模型的拟合效果更好;
(2)某位购房者拟于2018年6月份购买这个小区![]() 平方米的二手房(欲
平方米的二手房(欲
购房为其家庭首套房).若购房时该小区所有住房的房产证均已满2年但未满5年,请你利用(1)中拟合效果更好的模型估算该购房者应支付的购房金额.(购房金额=房款+税费;房屋均价精确到0.001万元/平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按房屋的计税价格进行征收.(计税价格=房款),征收方式见下表:
契税 (买方缴纳) | 首套面积90平方米以内(含90平方米)为1%;首套面积90平方米以上且144平方米以内(含144平方米)为1.5%;面积144平方米以上或非首套为3% |
增值税 (卖方缴纳) | 房产证未满2年或满2年且面积在144平方米以上(不含144平方米)为5.6%;其他情况免征 |
个人所得税 (卖方缴纳) | 首套面积144平方米以内(含144平方米)为1%;面积144平方米以上或非首套均为1.5%;房产证满5年且是家庭唯一住房的免征 |
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 参考公式:相关指数
. 参考公式:相关指数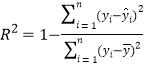 .
.
【答案】(1)见解析;(2)
【解析】分析:(1)由所给数据计算出![]() ,比较可得;
,比较可得;
(2)由(1)中较好的模型预测出均价,然后分类计算购房金额,可得结论.
详解:(1)设模型![]() 和
和![]() 的相关指数分别为
的相关指数分别为![]() 和
和![]() ,则
,则![]() ,
,![]() ,
,
所以模型![]() 拟合的效果好.
拟合的效果好.
(2)由(1)知模型![]() 拟合的效果好,利用该模型预测可得,这个小区在2018年6月份的在售二手房均价为
拟合的效果好,利用该模型预测可得,这个小区在2018年6月份的在售二手房均价为
![]() 万平方米
万平方米
设该购房者应支付的购房金额为![]() 万元,因为税费中买方只需缴纳契税,所以
万元,因为税费中买方只需缴纳契税,所以
①当![]() 时,契税为计税价格的
时,契税为计税价格的![]() ,
,
故![]() ;
;
②当![]() 时,契税为计税价格的
时,契税为计税价格的![]() ,
,
故![]() ;
;
③当![]() 时,契税为计税价格的
时,契税为计税价格的![]()
故![]() ;
;
所以

 阅读快车系列答案
阅读快车系列答案【题目】下表是某地某年月平均气温(华氏度):
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
平均气温 | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
以月份为x轴(![]() 月份
月份![]() ),以平均气温为y轴.
),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①![]() ;②
;②![]() ;③
;③![]() .
.