题目内容
已知函数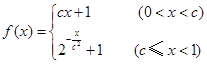 满足
满足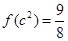 .
.
(1)求常数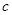 的值 ;
的值 ;
(2)解不等式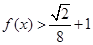 .
.
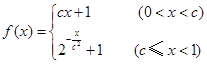 满足
满足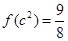 .
.(1)求常数
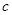 的值 ;
的值 ;(2)解不等式
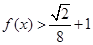 .
.(1) 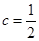 ;(2)
;(2)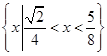
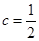 ;(2)
;(2)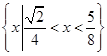
试题分析:(1)显然
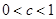 ,所以
,所以 ,代入相应解析式求出
,代入相应解析式求出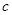 ;(2)由(1)确定函数解析式,对在不同段上的
;(2)由(1)确定函数解析式,对在不同段上的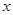 讨论.
讨论.试题解析:(1)因为
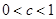 ,所以
,所以 ;由
;由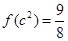 ,即
,即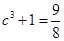 ,
,
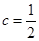 . 4分
. 4分(2)由(1)得
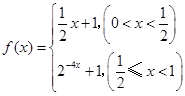 ,由
,由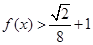 得, 6分
得, 6分当
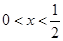 时,解得
时,解得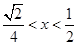 ; 8分
; 8分 当
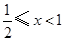 时,解得
时,解得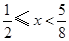 . 10分
. 10分所以
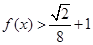 的解集为
的解集为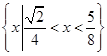 . 12分
. 12分
练习册系列答案
相关题目
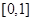 上的函数
上的函数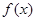 同时满足:①
同时满足:①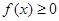 ;②
;②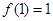 ;③若
;③若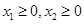 ,且
,且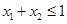 ,则
,则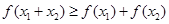 成立.则称函数
成立.则称函数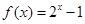 在区间
在区间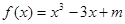 只有一个零点,则实数m的取值范围是( )
只有一个零点,则实数m的取值范围是( )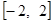
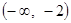 ∪
∪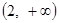
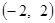
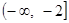 ∪
∪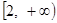
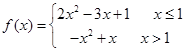 ,关于x的方程f(x)=m(m∈R)恰有三个互不相等的实数根
,关于x的方程f(x)=m(m∈R)恰有三个互不相等的实数根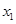 ,
,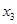 ,
,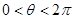 ,且方程
,且方程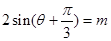 有两个不同的实数根,则这两个实根的和为 .
有两个不同的实数根,则这两个实根的和为 . 年(
年(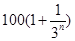 万元.设从2012年起的前
万元.设从2012年起的前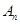 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).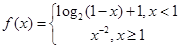 ,若
,若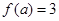 ,则
,则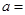 .
.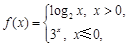 ,则
,则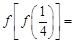 .
.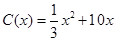 上的函数
上的函数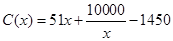 满足
满足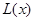 .若当
.若当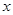 时.
时.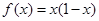 ,则当
,则当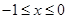 时,
时,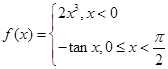 = .
= .