题目内容
椭圆M: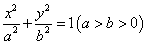 的左,右焦点分别为
的左,右焦点分别为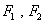 ,P为椭圆M上任一点,且
,P为椭圆M上任一点,且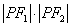 的最大值的取值范围是
的最大值的取值范围是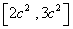 ,其中
,其中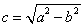 ,则椭圆M的离心率e的取值范围是________.
,则椭圆M的离心率e的取值范围是________.
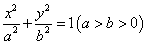 的左,右焦点分别为
的左,右焦点分别为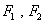 ,P为椭圆M上任一点,且
,P为椭圆M上任一点,且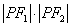 的最大值的取值范围是
的最大值的取值范围是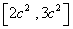 ,其中
,其中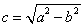 ,则椭圆M的离心率e的取值范围是________.
,则椭圆M的离心率e的取值范围是________.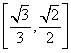
∵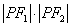 的最大值为
的最大值为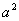 ,
,
∴由题意知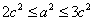 ,
,
∴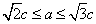 ,
,
∴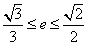 ,
,
∴椭圆离心率e的取值范围是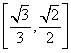 .
.
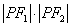 的最大值为
的最大值为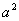 ,
,∴由题意知
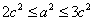 ,
,∴
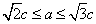 ,
,∴
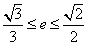 ,
,∴椭圆离心率e的取值范围是
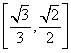 .
.
练习册系列答案
相关题目
题目内容
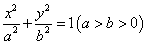 的左,右焦点分别为
的左,右焦点分别为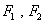 ,P为椭圆M上任一点,且
,P为椭圆M上任一点,且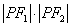 的最大值的取值范围是
的最大值的取值范围是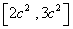 ,其中
,其中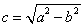 ,则椭圆M的离心率e的取值范围是________.
,则椭圆M的离心率e的取值范围是________.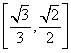
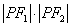 的最大值为
的最大值为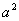 ,
,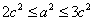 ,
,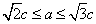 ,
,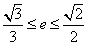 ,
,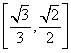 .
.