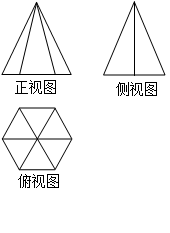
题目内容
(本题满分12分)
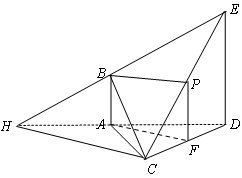
如图,已知AB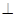 平面ACD,DE∥AB,△ACD是正三角形,
平面ACD,DE∥AB,△ACD是正三角形,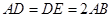 ,且F是CD的中点.
,且F是CD的中点.
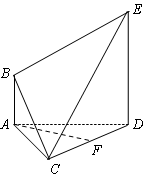
(Ⅰ)求证AF∥平面BCE;
(Ⅱ)设AB=1,求多面体ABCDE的体积.
如图,已知AB
 平面ACD,DE∥AB,△ACD是正三角形,
平面ACD,DE∥AB,△ACD是正三角形,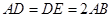 ,且F是CD的中点.
,且F是CD的中点.
(Ⅰ)求证AF∥平面BCE;
(Ⅱ)设AB=1,求多面体ABCDE的体积.
解:(Ⅰ)见解析;(II)多面体ABCDE的体积为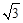 .
.
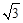 .
.本试题主要是考查了线面平行的判定定理和多面体体积的求解的综合运用。
(1)因为取CE中点P,连结FP、BP,∵F为CD的中点,∴FP//DE,且FP=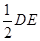
又AB//DE,且AB=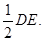 ∴AB//FP,且AB=FP,
∴AB//FP,且AB=FP,
∴ABPF为平行四边形,
∴AF//BP,从而利用判定定理得到证明。
(2)根据已知中直角梯形ABED的面积和C到平面ABDE的距离,然后表示出锥体的体积。
解:(Ⅰ)取CE中点P,连结FP、BP,
∵F为CD的中点,∴FP//DE,且FP=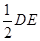 .
.
又AB//DE,且AB=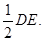 ∴AB//FP,且AB=FP,
∴AB//FP,且AB=FP,
∴ABPF为平行四边形,
∴AF//BP.
又∵AF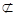 平面BCE,BP
平面BCE,BP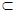 平面BCE,
平面BCE,
∴AF//平面BCE.
(II)∵直角梯形ABED的面积为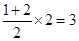 ,
,
C到平面ABDE的距离为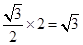 ,
,
∴四棱锥C-ABDE的体积为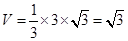 .即多面体ABCDE的体积为
.即多面体ABCDE的体积为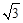 .
.
(1)因为取CE中点P,连结FP、BP,∵F为CD的中点,∴FP//DE,且FP=
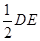
又AB//DE,且AB=
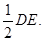 ∴AB//FP,且AB=FP,
∴AB//FP,且AB=FP,∴ABPF为平行四边形,
∴AF//BP,从而利用判定定理得到证明。
(2)根据已知中直角梯形ABED的面积和C到平面ABDE的距离,然后表示出锥体的体积。
解:(Ⅰ)取CE中点P,连结FP、BP,

∵F为CD的中点,∴FP//DE,且FP=
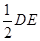 .
.又AB//DE,且AB=
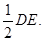 ∴AB//FP,且AB=FP,
∴AB//FP,且AB=FP,∴ABPF为平行四边形,
∴AF//BP.
又∵AF
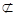 平面BCE,BP
平面BCE,BP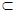 平面BCE,
平面BCE, ∴AF//平面BCE.
(II)∵直角梯形ABED的面积为
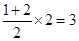 ,
,C到平面ABDE的距离为
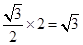 ,
,∴四棱锥C-ABDE的体积为
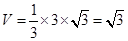 .即多面体ABCDE的体积为
.即多面体ABCDE的体积为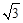 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

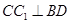
 ,那么正方体的棱长等于( )
,那么正方体的棱长等于( )



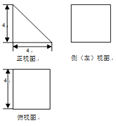
 中, 底面是以∠ABC为直角的等腰三角形, 点
中, 底面是以∠ABC为直角的等腰三角形, 点 在平面ABC上的射影为AC的中点D, AC=2,
在平面ABC上的射影为AC的中点D, AC=2, =3,则
=3,则 与底面ABC所成角的正切值为 .
与底面ABC所成角的正切值为 . 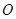 引向量
引向量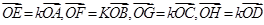 ,
,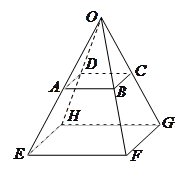
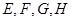 共面;
共面; 平面EFGH.
平面EFGH.