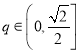Question

【题目】若函数f（x）＝x2+x﹣lnx+1在其定义域的一个子区间（2k﹣1，k+2）内不是单调函数，则实数k的取值范围是___．

Answer 1

【答案】.

【解析】

根据题意，求出函数的定义域，由区间（2k﹣1，k+2）为其定义域的一个子区间得到关于的不等式，对函数进行求导，利用导数判断函数的单调区间，结合函数在区间（2k﹣1，k+2）上不单调得到关于的不等式，然后取交集即可.

由题意知，函数f（x）＝x2+x﹣lnx+1的定义域为（0，+∞），

由区间（2k﹣1，k+2）为其定义域的一个子区间，可得：0≤2k﹣1＜k+2，解得≤k＜3，

f′（x）＝2x+1﹣，令f′（x）＝0，解得x＝，

所以当时，，函数在上单调递减；

当时，，函数在上单调递增，

∵函数f（x）＝x2+x﹣lnx+1在其定义域的一个子区间（2k﹣1，k+2）内不是单调函数，

∴2k﹣1＜＜k+2，解得：﹣＜k＜，与≤k＜3联立解得：≤k＜．

故答案为：.