题目内容
【题目】某公司推出一新款手机，因其功能强大，外观新潮，一上市便受到消费者争相抢购，销量呈上升趋势.散点图是该款手机上市后前6周的销售数据.
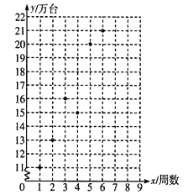
（Ⅰ）根据散点图，用最小二乘法求
关于
的线性回归方程，并预测该款手机第8周的销量；
（Ⅱ）为了分析市场趋势，该公司市场部从前6周的销售数据中随机抽取2周的数据，求抽到的这2周的销量均在20万台以下的概率.
参考公式：回归直线方程
，其中：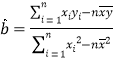
，
.
【答案】（Ⅰ）
，25万台（Ⅱ）
【解析】
（Ⅰ）根据散点图中的数据求出
，再结合所给公式求出
，即可得到所求回归方程，进而可进行预测；（Ⅱ）列举出所有的基本事件和事件“抽到的这2周的销量均在20万台以下”包含的基本事件，然后根据古典概型概率求解即可．
（Ⅰ）由题意得
，
，
，
，
，
.
所以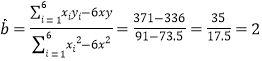
，
所以
．
所以所求的线性回归直线方程为.
当
时，
，所以预计该款手机第8周的销量为25万台．
（Ⅱ）由题意可知，前6周中有4周销量在20万台以下，分别记为
，
，
，
，有2周的销量不在20万台以下，分别记为
，
．
从中随机抽取2周的所有基本事件为：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共15个．
设事件
为“抽到的这2周的销量均在20万台以下”，则事件包含的基本事件有：，，，，，，共6个．
所以
，
即抽到的这2周的销量均在20万台以下的概率为．
练习册系列答案
相关题目
