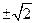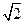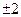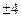题目内容
已知圆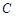 :
: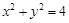 .
.
⑴直线 过点
过点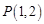 ,且与圆
,且与圆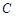 交于
交于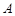 、
、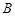 两点,若
两点,若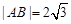 ,求直线
,求直线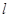 的方程;
的方程;
⑵过圆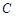 上一动点
上一动点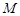 作平行于
作平行于 轴的直线
轴的直线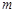 ,设
,设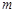 与
与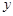 轴的交点为
轴的交点为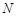 ,若向量
,若向量 ,求动点
,求动点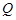 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
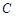 :
: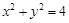 .
.⑴直线
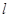 过点
过点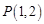 ,且与圆
,且与圆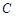 交于
交于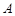 、
、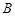 两点,若
两点,若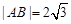 ,求直线
,求直线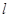 的方程;
的方程;⑵过圆
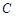 上一动点
上一动点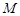 作平行于
作平行于 轴的直线
轴的直线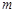 ,设
,设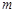 与
与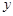 轴的交点为
轴的交点为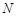 ,若向量
,若向量 ,求动点
,求动点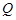 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.(1)
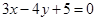 或
或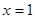 .
.(2)轨迹是焦点坐标为
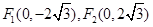 ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉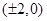 两点.
两点.⑴①当直线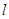 垂直于
垂直于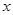 轴时,则此时直线方程为
轴时,则此时直线方程为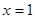 ,
,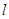 与圆的两个交点坐标为
与圆的两个交点坐标为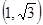 和
和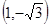 ,其距离为
,其距离为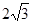 ,满足题意.
,满足题意.
②若直线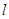 不垂直于
不垂直于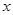 轴,设其方程为
轴,设其方程为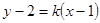 ,即
,即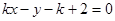
设圆心到此直线的距离为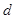 ,则
,则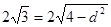 ,得
,得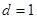 ∴
∴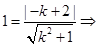
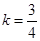 ,
,
故所求直线方程为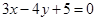 综上所述,所求直线为
综上所述,所求直线为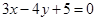 或
或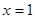 .
.
⑵设点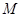 的坐标为
的坐标为 ,
,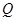 点坐标为
点坐标为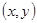 , 则
, 则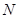 点坐标是
点坐标是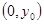 .
.
∵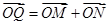 ,∴
,∴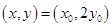 即
即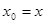 ,
,
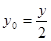
又∵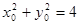 ,∴
,∴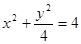 由已知,直线m //ox轴,所以,
由已知,直线m //ox轴,所以,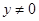 ,
,
∴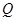 点的轨迹方程是
点的轨迹方程是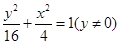 ,
,
轨迹是焦点坐标为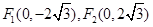 ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉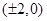 两点.
两点.
 垂直于
垂直于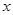 轴时,则此时直线方程为
轴时,则此时直线方程为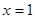 ,
,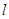 与圆的两个交点坐标为
与圆的两个交点坐标为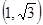 和
和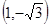 ,其距离为
,其距离为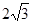 ,满足题意.
,满足题意. ②若直线
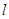 不垂直于
不垂直于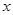 轴,设其方程为
轴,设其方程为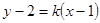 ,即
,即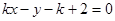
设圆心到此直线的距离为
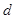 ,则
,则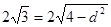 ,得
,得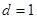 ∴
∴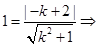
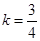 ,
,故所求直线方程为
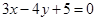 综上所述,所求直线为
综上所述,所求直线为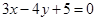 或
或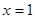 .
.⑵设点
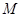 的坐标为
的坐标为 ,
,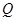 点坐标为
点坐标为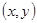 , 则
, 则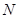 点坐标是
点坐标是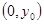 .
.∵
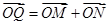 ,∴
,∴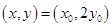 即
即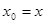 ,
,
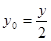
又∵
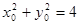 ,∴
,∴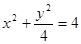 由已知,直线m //ox轴,所以,
由已知,直线m //ox轴,所以,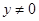 ,
, ∴
 点的轨迹方程是
点的轨迹方程是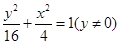 ,
, 轨迹是焦点坐标为
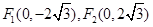 ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉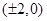 两点.
两点.
练习册系列答案
相关题目
 轴相切,圆心在直线
轴相切,圆心在直线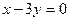 上,在
上,在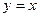 上截得的弦长为
上截得的弦长为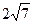 ,求此圆的方程.
,求此圆的方程.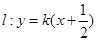 与圆
与圆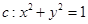 的位置关系是 ( )
的位置关系是 ( )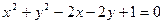 上的点到直线
上的点到直线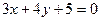 的距离最大值是
的距离最大值是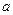 ,最小值是
,最小值是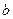 ,则
,则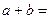 ( )
( )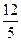
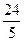
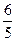
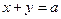 与圆
与圆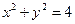 交于A、B两点,O是坐标原点,向量
交于A、B两点,O是坐标原点,向量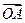 、
、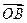 满足
满足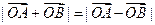 ,则实数a的值是( )
,则实数a的值是( )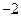
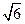 或
或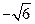
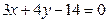 与圆
与圆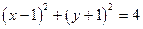 的位置关系是( )
的位置关系是( )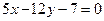 相切的圆的方程为_____________
相切的圆的方程为_____________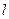 过点
过点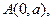 斜率为1,圆
斜率为1,圆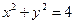 上恰有3个点到
上恰有3个点到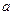 的值为( )
的值为( )