题目内容
已知数列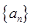 ,
,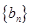 满足
满足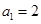 ,
,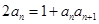 ,
,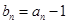 ,数列
,数列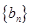 的前
的前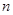 项和为
项和为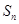 ,
,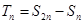 .
.
(1)求数列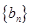 的通项公式;
的通项公式;
(2)求证: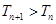 ;
;
(3)求证:当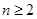 时,
时,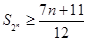 .
.
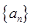 ,
,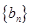 满足
满足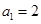 ,
,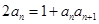 ,
,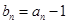 ,数列
,数列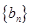 的前
的前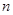 项和为
项和为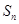 ,
,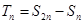 .
.(1)求数列
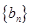 的通项公式;
的通项公式;(2)求证:
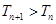 ;
;(3)求证:当
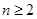 时,
时,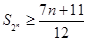 .
.(1) ,(2)详见解析,(3)详见解析.
,(2)详见解析,(3)详见解析.
 ,(2)详见解析,(3)详见解析.
,(2)详见解析,(3)详见解析.试题分析:(1)求数列
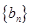 的通项公式,需先探究数列
的通项公式,需先探究数列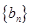 的递推关系,由
的递推关系,由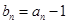 ,得
,得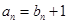 ,代入
,代入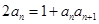 ,得
,得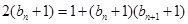 ,∴
,∴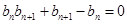 ,从而有
,从而有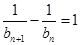 ,∵
,∵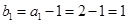 ,∴
,∴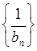 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴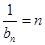 ,即
,即 .(2)∵
.(2)∵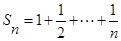 ,∴
,∴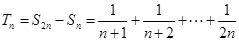 ,
,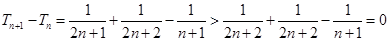 ,∴
,∴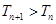 .(3)∵
.(3)∵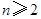 ,∴
,∴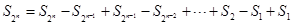
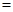
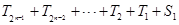 .由(2)知
.由(2)知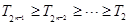 ,∴
,∴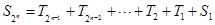
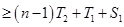
∵
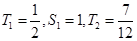 ,所以
,所以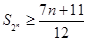
解:(1)由
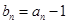 ,得
,得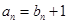 ,代入
,代入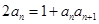 ,
,得
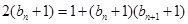 ,
,∴

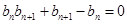 ,从而有
,从而有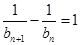 ,
,∵
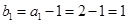 ,
,∴
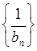 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴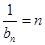 ,即
,即 .
. (2)∵
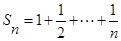 ,∴
,∴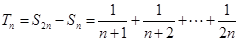 ,
,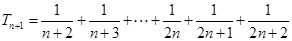 ,
,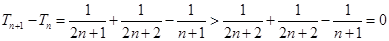 ,
,∴
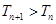 .
. (3)∵
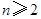 ,
,∴
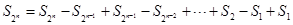
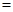
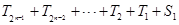 .
.由(2)知
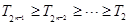 ,∵
,∵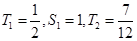 ,
,∴
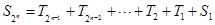
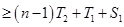
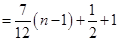
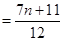 .
. 
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
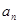 }、{
}、{ 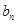 }满足:
}满足: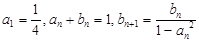 .
.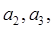
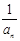 }为等差数列,并求数列
}为等差数列,并求数列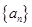 和{
和{ 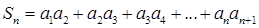 ,求实数
,求实数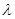 为何值时
为何值时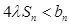 恒成立.
恒成立.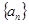 满足
满足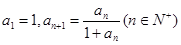
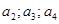 的值。
的值。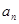 ,并用数学归纳法证明。
,并用数学归纳法证明。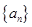 的前
的前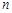 项和
项和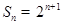 ,数列
,数列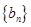 满足
满足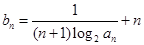 .
.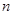 项和
项和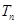 .
.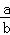 的值是( )
的值是( )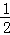
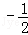
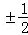
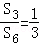 ,则
,则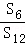 =( )
=( )