题目内容
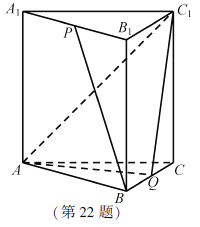
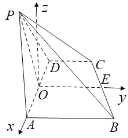
【题目】如图，在四棱锥
中，底面ABCD为梯形，AB//CD，
，AB=AD=2CD=2，△ADP为等边三角形．
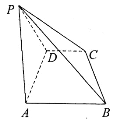
(1)当PB长为多少时，平面
平面ABCD?并说明理由；
(2)若二面角
大小为150°，求直线AB与平面PBC所成角的正弦值．
【答案】（1）当
时，平面
平面
，详见解析（2）
【解析】
(1)根据平面和平面垂直可得线面垂直，从而可得
,利用直角三角形知识可得
的长；
(2)构建空间直角坐标系，利用法向量求解直线AB与平面PBC所成角的正弦值.
解：（1）当时，平面平面，
证明如下：在
中，因为
，所以，
又
，
，所以
平面
，
又
平面，所以平面平面；
（2）分别取线段
的中点
，连接
，因为
为等边三角形，
为
的中点，所以
，
为的中点，所以
,
又，所以
，故
为二面角
的平面角，所以
，
如图，分别以
的方向以及垂直于平面向上的方向作为
轴的正方向，建立空间直角坐标系
，
因为
，，所以
，
，
，
.
可得
，
，
设
为平面
的一个法向量，则有
，
即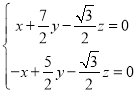
，令
，
可得
，
设
与平面
所成角为
，则有
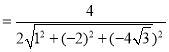
所以直线与平面所成角的正弦值为.
快乐5加2金卷系列答案
【题目】手机支付也称为移动支付，是指允许用户使用其移动终端（通常是手机）对所消费的商品或服务进行账务支付的一种服务方式．随着信息技术的发展，手机支付越来越成为人们喜欢的支付方式．某机构对某地区年龄在15到75岁的人群“是否使用手机支付”的情况进行了调查，随机抽取了100人，其年龄频率分布表和使用手机支付的人数如下所示：（年龄单位：岁）
年龄段 | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75] |
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
使用人数 | 8 | 28 | 24 | 12 | 2 | 1 |
（1）若以45岁为分界点，根据以上统计数据填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.001的前提下认为“使用手机支付”与年龄有关？
年龄低于45岁 | 年龄不低于45岁 | |
使用手机支付 | ||
不使用手机支付 |
（2）若从年龄在[55，65），[65，75]的样本中各随机选取2人进行座谈，记选中的4人中“使用手机支付”的人数为X，求随机变量X的分布列和数学期望．
参考数据：
P（K2≥k0） | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式：
．
