题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 是偶函数,求实数
是偶函数,求实数![]() 的值;
的值;
(2)若函数![]() ,关于
,关于![]() 的方程
的方程![]() 有且只有一个实数根,求实数
有且只有一个实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据偶函数的定义建立方程关系即可求![]() 的值;
的值;
(2)根据题意方程![]() 有且只有一个实数根,等价于
有且只有一个实数根,等价于![]() 只有一个实数根,等价于
只有一个实数根,等价于![]() 有且只有一个实数根,令,
有且只有一个实数根,令,![]() 则需关于
则需关于![]() 的方程
的方程![]() 有且只有一个大于
有且只有一个大于![]() 的实数根,结合二次函数的性质来分析。
的实数根,结合二次函数的性质来分析。
解:(1)因为![]() 是偶函数,
是偶函数,
所以![]() 对任意的
对任意的![]() 成立,
成立,
所以![]() 对任意的
对任意的![]() 成立,
成立,
所以![]() 对任意的
对任意的![]() 成立,
成立,
所以![]() .
.
(2)因为![]() ,
,![]() ,
,
所以![]() ,
,
所以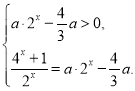
设![]() ,则有关于
,则有关于![]() 的方程
的方程![]() .
.
若![]() ,即
,即![]() ,则需关于
,则需关于![]() 的方程
的方程![]() 有且只有一个大于
有且只有一个大于![]() 的实数根.
的实数根.
设![]() ,则
,则![]() ,
,
所以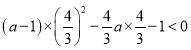 ,
,
所以![]() 成立,
成立,
所以![]() ,满足题意;
,满足题意;
若![]() ,即
,即![]() 时,解得
时,解得![]() ,不满足题意;
,不满足题意;
若![]() ,即
,即![]() 时,
时,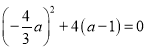 ,且
,且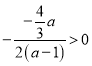 ,
,
所以![]() .
.
当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有且只有一个实数根
有且只有一个实数根![]() ,满足题意.
,满足题意.
综上,所求实数![]() 的取值范围是
的取值范围是![]() ..
..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在![]() 层班级,生物在
层班级,生物在![]() 层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
第一节 | 第二节 | 第三节 | 第四节 |
地理 | 化学 | 地理 | 化学 |
生物 | 化学 | 生物 | 历史 |
物理 | 生物 | 物理 | 生物 |
物理 | 生物 | 物理 | 物理 |
政治1班 | 物理 | 政治2班 | 政治3班 |
A.8种B.10种C.12种D.14种