题目内容
【题目】在直角坐标系xOy中,已知点A(a,a),B(2,3),C(3,2).
(1)若向量 ![]() ,
, ![]() 的夹角为钝角,求实数a的取值范围;
的夹角为钝角,求实数a的取值范围;
(2)若a=1,点P(x,y)在△ABC三边围成的区域(含边界)上, ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),求m﹣n的最大值.
(m,n∈R),求m﹣n的最大值.
【答案】
(1)解:由A(a,a),B(2,3),C(3,2).
得 ![]() ,
,
由题意, 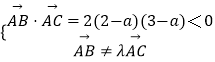 ,
,
得2<a<3且a ![]() ,
,
∴ ![]()
(2)解:a=1时,A(1,1),B(2,3),C(3,2).
作出△ABC三边围成的区域如图:

∵ ![]() ,∴(x,y)=m(1,2)+n(2,1),
,∴(x,y)=m(1,2)+n(2,1),
即x=m+2n,y=2m+n,解得m﹣n=y﹣x,令y﹣x=t,
由图知,当直线y=x+t过点B(2,3)时,t取得最大值1,故m﹣n的最大值为1
【解析】(1)由已知点的坐标求出 ![]() 的坐标,再由向量
的坐标,再由向量 ![]() ,
, ![]() 的夹角为钝角可得
的夹角为钝角可得 ![]() <0,且A、B、C不共线,由此列式求得实数a的取值范围;(2)画出△ABC三边围成的区域,结合
<0,且A、B、C不共线,由此列式求得实数a的取值范围;(2)画出△ABC三边围成的区域,结合 ![]() =m
=m ![]() +n
+n ![]() 可得x=m+2n,y=2m+n,解得m﹣n=y﹣x,令y﹣x=t,再由线性规划知识求得m﹣n的最大值.
可得x=m+2n,y=2m+n,解得m﹣n=y﹣x,令y﹣x=t,再由线性规划知识求得m﹣n的最大值.
【考点精析】掌握平面向量的基本定理及其意义是解答本题的根本,需要知道如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.

练习册系列答案
相关题目


