题目内容
【题目】已知数列{an}的前n项和为 ![]() .
.
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数a的值及an;
(3)对于(2)中的an , 记f(n)=λa2n+1﹣4λan+1﹣3,若f(n)<0对任意的正整数n恒成立,求实数λ的取值范围.
【答案】
(1)解:∵数列{an}的前n项和为 ![]() ,
,
∴a1=S1=2+a,
S2=(2+a)+a2=4+a,解得a2=2,
a3=S3﹣S2=8﹣4=4
(2)解:∵数列{an}为等比数列,
由(1)知a1=2+a,a2=2,a3=4,
∴ ![]() ,即4=(2+a)4,
,即4=(2+a)4,
解得a=﹣1.
∴ ![]() ,
,
∴ ![]()
(3)解:∵ ![]() ,
,
∴f(n)=λa2n+1﹣4λan+1﹣3
=λ22n﹣4λ2n﹣3
=λ(2n﹣2)2﹣3﹣4λ<0,
即λ[(2n﹣2)2﹣4]<3,
分3种情况讨论:
①、λ>0时,有λ< ![]() ≤﹣
≤﹣ ![]() ,解可得,λ<﹣
,解可得,λ<﹣ ![]() ,此时无解;
,此时无解;
②、λ=0时,有f(n)<0恒成立,即λ=0符合题意;
③、λ<0时,有λ> ![]() ,解可得,λ>﹣
,解可得,λ>﹣ ![]() ,
,
此时λ的取值范围是﹣ ![]() <λ<0;
<λ<0;
∴综合可得:实数λ的取值范围是(﹣ ![]() ,0]
,0]
【解析】(1)利用 ![]() 能求出a1 , a2 , a3 . (2)由数列{an}为等比数列,得到
能求出a1 , a2 , a3 . (2)由数列{an}为等比数列,得到 ![]() ,由此能求出常数a的值及an . (3)由
,由此能求出常数a的值及an . (3)由 ![]() ,得到f(n)=λ(2n﹣2)2﹣3﹣4λ,由此能求出结果.
,得到f(n)=λ(2n﹣2)2﹣3﹣4λ,由此能求出结果.
【考点精析】关于本题考查的数列的前n项和和等比数列的基本性质,需要了解数列{an}的前n项和sn与通项an的关系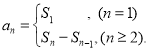 ;{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列才能得出正确答案.
;{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列才能得出正确答案.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目