题目内容
(2014·佛山模拟)数列{an}满足an+an+1= (n∈N*),a2=2,Sn是数列{an}的前n项和,则S2015为( )
(n∈N*),a2=2,Sn是数列{an}的前n项和,则S2015为( )
 (n∈N*),a2=2,Sn是数列{an}的前n项和,则S2015为( )
(n∈N*),a2=2,Sn是数列{an}的前n项和,则S2015为( )| A.502 | B.504 | C.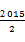 | D.2015 |
A
因为an+an+1= (n∈N*),
(n∈N*),
所以a1= -a2=
-a2= -2,a2=2,a3=
-2,a2=2,a3= -2,a4=2,…
-2,a4=2,…
故a2n=2,a2n-1= -2,
-2,
所以S2015=1008a1+1007a2=1008×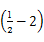 +1007×2=502.
+1007×2=502.
 (n∈N*),
(n∈N*),所以a1=
 -a2=
-a2= -2,a2=2,a3=
-2,a2=2,a3= -2,a4=2,…
-2,a4=2,…故a2n=2,a2n-1=
 -2,
-2,所以S2015=1008a1+1007a2=1008×
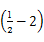 +1007×2=502.
+1007×2=502.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
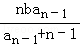 (n≥2)
(n≥2)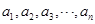 为
为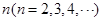 阶“期待数列”:
阶“期待数列”: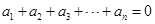 ,②
,②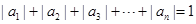 .
.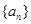 为
为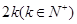 阶“期待数列”,求公比
阶“期待数列”,求公比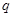 ;
;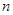 阶“期待数列”
阶“期待数列”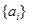 的前
的前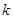 项和为
项和为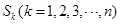 .
.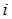 )求证:
)求证: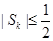 ;
;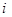
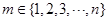 ,使
,使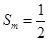 ,试问数列
,试问数列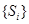
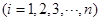 是否为
是否为 是首项
是首项 ,公比为
,公比为 的等比数列,
的等比数列,

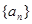 中,
中,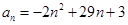 (
(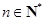 ),那么此数列
),那么此数列
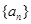 的前
的前 项和
项和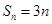 ,则此数列的通项公式为____________________.
,则此数列的通项公式为____________________.