题目内容
已知点P是抛物线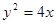
上的点，设点P到抛物线准线的距离为
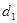，到圆
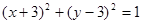上一动点Q的距离为
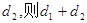的最小值是
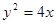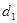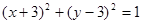上的点，设点P到抛物线准线的距离为，到圆上一动点Q的距离为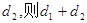的最小值是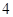 
解：连接抛物线的焦点与圆心，由抛物线的定义知这两点连线的长度减去圆的半径即我所求的最小距离，∵抛物线的焦点是（1，0），圆心是（-3，3），∴d1+d2的最小值是4。
练习册系列答案
相关题目
题目内容
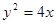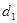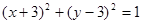上的点，设点P到抛物线准线的距离为，到圆上一动点Q的距离为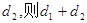的最小值是 
的准线方程为 
=4x，F是C的焦点，过焦点F的直线l与C交于 A，B两点，O为坐标原点。
·
的值；（2）设
=
，求△ABO的面积S的最小值；
，求
的抛物线的标准方程为 （ ）
是抛物线
（p>0）的内接正三角形（
为坐标原点），其面积为
；点M是直线
：
上的动点，过点M作抛物线的切线MP、MQ，P、Q为切点．
MPQ面积的最小值及相应的直线PQ的方程．
是抛物线
上的一点,过
点的切线方程的斜率可通过如下方式求得: 在
两边同时对x求导,得:
，所以过
,试用上述方法求出双曲线
在
处的切线方程为___________.
的焦点到其准线的距离为 .
的焦点为F，若M是抛物线上的动点，则
的最大值为 .