题目内容
已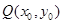 是抛物线
是抛物线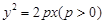 上的一点,过
上的一点,过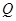 点的切线方程的斜率可通过如下方式求得: 在
点的切线方程的斜率可通过如下方式求得: 在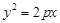 两边同时对x求导,得:
两边同时对x求导,得: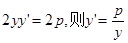 ,所以过
,所以过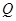 的切线的斜率:
的切线的斜率: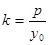 ,试用上述方法求出双曲线
,试用上述方法求出双曲线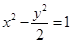 在
在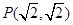 处的切线方程为___________.
处的切线方程为___________.
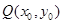 是抛物线
是抛物线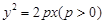 上的一点,过
上的一点,过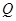 点的切线方程的斜率可通过如下方式求得: 在
点的切线方程的斜率可通过如下方式求得: 在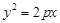 两边同时对x求导,得:
两边同时对x求导,得: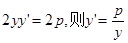 ,所以过
,所以过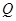 的切线的斜率:
的切线的斜率: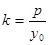 ,试用上述方法求出双曲线
,试用上述方法求出双曲线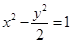 在
在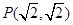 处的切线方程为___________.
处的切线方程为___________.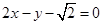
解:由双曲线x2-y2/2 =1,得到y2=2x2-2,
根据题意,两边同时对x求导得:2yy′=4x,解得y′="2x" /y ,
由P( 2 ,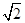 ),得到过P得切线的斜率k=2,
),得到过P得切线的斜率k=2,
则所求的切线方程为:y-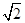 =2(x- 2 ),即2x-y-
=2(x- 2 ),即2x-y- 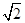 =0.
=0.
故答案为:2x-y-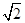 =0
=0
根据题意,两边同时对x求导得:2yy′=4x,解得y′="2x" /y ,
由P( 2 ,
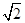 ),得到过P得切线的斜率k=2,
),得到过P得切线的斜率k=2,则所求的切线方程为:y-
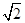 =2(x- 2 ),即2x-y-
=2(x- 2 ),即2x-y- 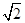 =0.
=0.故答案为:2x-y-
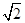 =0
=0
练习册系列答案
相关题目
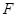 是抛物线
是抛物线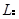
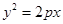
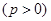 的焦点,
的焦点,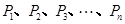 是抛物线
是抛物线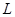 上的
上的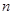 个不同的点(
个不同的点(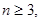
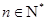 ).
).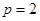 时,试写出抛物线
时,试写出抛物线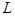 上的三个定点
上的三个定点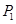 、
、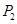 、
、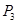 的坐标,从而使得
的坐标,从而使得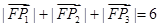 ;
;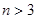 时,若
时,若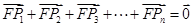 ,
, ;
;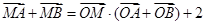 .
.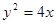 上的点,设点P到抛物线准线的距离为
上的点,设点P到抛物线准线的距离为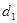 ,到圆
,到圆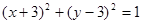 上一动点Q的距离为
上一动点Q的距离为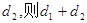 的最小值是
的最小值是  为抛物线
为抛物线 上不同两点,且直线
上不同两点,且直线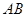 倾斜角为锐角,
倾斜角为锐角, 为抛物线焦点,若
为抛物线焦点,若 则直线
则直线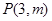 在以点
在以点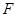 为焦点的抛物线
为焦点的抛物线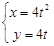 (
(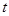 为参数)上,则
为参数)上,则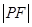 等于( )
等于( ) 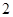
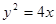 上的两点,O是抛物线的顶点,OA⊥OB.
上的两点,O是抛物线的顶点,OA⊥OB.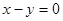 的距离的最小值.
的距离的最小值. 的线段AB的两个端点A、B都在抛物线
的线段AB的两个端点A、B都在抛物线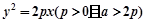 上滑动,则线段AB的中点M到
上滑动,则线段AB的中点M到 轴的最短距离是
轴的最短距离是 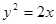 内一点A(1,1)作弦BC,若A为BC的中点,则直线BC的方程为
内一点A(1,1)作弦BC,若A为BC的中点,则直线BC的方程为