题目内容
(本题满分14分)
设函数
(1)求函数 极值;
极值;
(2)当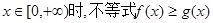 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
设函数

(1)求函数
 极值;
极值;(2)当
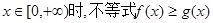 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. (1)f极大=f(—1)=—4. f极小=f(—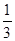 )=
)=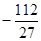 ;(2)a的范围为
;(2)a的范围为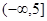 。
。
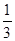 )=
)=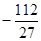 ;(2)a的范围为
;(2)a的范围为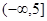 。
。本题考查利用导数研究函数的极值以及由函数恒成立的问题求参数的取值范围,求解本题关键是记忆好求导的公式以及极值的定义,对于函数的恒成立的问题求参数,要注意正确转化,恰当的转化可以大大降低解题难度.
(Ⅰ)先求出函数的导数,再令导数大于0求出单调增区间,导数小于0求出函数的减区间,再由极值的定义判断出极值即可;
(2)设F(x)=f(x)—g(x)=x3+(2—a)x2+4
利用不等式恒成立构造新函数,求解函数的最值得到结论。
解:(1)∵f(x)=x3+2x2+x—4
∴ =3x2+4x+1,…………………………2分
=3x2+4x+1,…………………………2分
令 =0,得x1= —1,x2= —
=0,得x1= —1,x2= —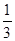 .
.
∴f极大=f(—1)=—4. f极小=f(—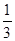 )=
)=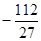 …………………………6分
…………………………6分
(2)设F(x)=f(x)—g(x)=x3+(2—a)x2+4
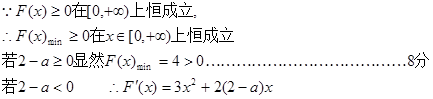
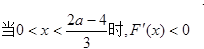
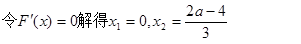
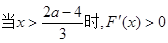
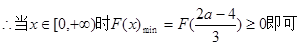
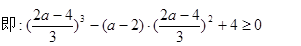
解得a≤5 ∴2<a≤5………10分,当x=0时,F(x)=4
∴a的范围为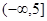 …………14分
…………14分
(Ⅰ)先求出函数的导数,再令导数大于0求出单调增区间,导数小于0求出函数的减区间,再由极值的定义判断出极值即可;
(2)设F(x)=f(x)—g(x)=x3+(2—a)x2+4
利用不等式恒成立构造新函数,求解函数的最值得到结论。
解:(1)∵f(x)=x3+2x2+x—4
∴
 =3x2+4x+1,…………………………2分
=3x2+4x+1,…………………………2分令
 =0,得x1= —1,x2= —
=0,得x1= —1,x2= —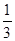 .
.| x | (-∞,-1) | -1 | (-1,-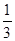 ) ) | -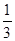 | (-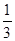 ,+∞) ,+∞) |
 | + | 0 | — | 0 | + |
 |  | 极大 |  | 极小 | 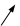 |
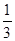 )=
)=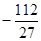 …………………………6分
…………………………6分(2)设F(x)=f(x)—g(x)=x3+(2—a)x2+4
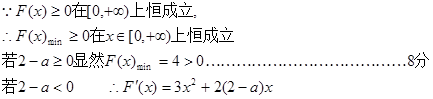
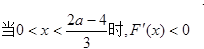
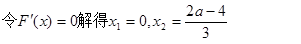
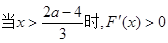
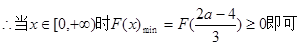
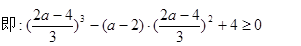
解得a≤5 ∴2<a≤5………10分,当x=0时,F(x)=4
∴a的范围为
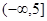 …………14分
…………14分
练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
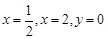 ,及曲线
,及曲线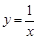 所围图形的面积为( )
所围图形的面积为( )



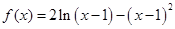 .
.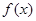 的单调递增区间;
的单调递增区间;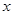 的方程
的方程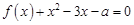 在区间
在区间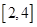 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数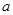 的取值范围.
的取值范围. 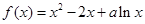 。
。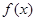 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数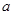 的取值范围;
的取值范围;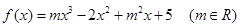 且
且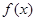 在
在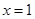 处取得极小值.
处取得极小值.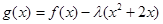 在
在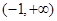 上是增函数,求实数
上是增函数,求实数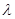 的取值范围。
的取值范围。 的导函数是
的导函数是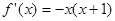 ,则函数
,则函数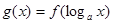
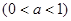

 ,
,

 ,
,
 为奇函数,
为奇函数,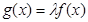
 在
在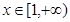 上恒成立,求
上恒成立,求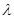 的取值范围。
的取值范围。 在区间
在区间 上是减函数,则
上是减函数,则 的最小值是( )
的最小值是( )  是减函数的区间为( )
是减函数的区间为( )

