ЬтФПФкШн
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж13ЗжЃЉШчЭМЫљЪОЕФОЅвЖЭММЧТМСЫМзЁЂввСНзщИїЫФУћЭЌбЇЕФЭЖРКУќжаДЮЪ§, ввзщМЧТМжагавЛИіЪ§ОнФЃК§ЃЌЮоЗЈШЗШЯ, дкЭМжавд![]() БэЪО.
БэЪО.

ЃЈЂёЃЉШчЙћввзщЭЌбЇЭЖРКУќжаДЮЪ§ЕФЦНОљЪ§ЮЊ![]() , Чѓ
, Чѓ![]() МАввзщЭЌбЇЭЖРКУќжаДЮЪ§ЕФЗНВю;
МАввзщЭЌбЇЭЖРКУќжаДЮЪ§ЕФЗНВю;
ЃЈЂђЃЉдкЃЈЂёЃЉЕФЬѕМўЯТ, ЗжБ№ДгМзЁЂввСНзщЭЖРКУќжаДЮЪ§ЕЭгк10ДЮЕФЭЌбЇжа,ИїЫцЛњбЁШЁвЛУћ, МЧЪТМўAЃКЁАСНУћЭЌбЇЕФЭЖРКУќжаДЮЪ§жЎКЭЮЊ17ЁБ, ЧѓЪТМўAЗЂЩњЕФИХТЪ.
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈЂђЃЉ
ЃЛЃЈЂђЃЉ![]() .
.
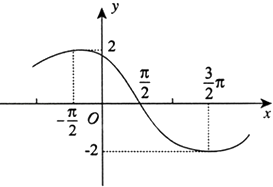
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈЂёЃЉРћгУЦНОљЪ§ЙЋЪНМДПЩЧѓЕУx,РћгУЗНВюЕФМЦЫуЙЋЪНМДПЩЧѓЕУЗНВю
ЃЈЂђЃЉСаГіетСНУћЭЌбЇЕФЭЖРКУќжаДЮЪ§жЎКЭЮЊ17ЕФЫљвдЪБМфРћгУЙХЕфИХаЭМДПЩЧѓГіИХТЪ
ЪдЬтНтЮіЃКЃЈЂёЃЉгЩЬтПЩЕУ![]() ЃЌ
ЃЌ
ЗНВю![]()
ЃЈЂђЃЉМЧМззщЭЖРКУќжаДЮЪ§ЕЭгк10ДЮЕФЭЌбЇЮЊ![]() ЃЌЫћУЧЕФЭЖРКУќжаДЮЪ§ЗжБ№ЮЊ9,7
ЃЌЫћУЧЕФЭЖРКУќжаДЮЪ§ЗжБ№ЮЊ9,7
МЧввзщЭЖРКУќжаДЮЪ§ЕЭгк10ДЮЕФЭЌбЇ![]() ЃЌЫћУЧЕФЭЖРКУќжаДЮЪ§ЗжБ№ЮЊ8ЃЌ8,9ЃЌгЩЬтвт
ЃЌЫћУЧЕФЭЖРКУќжаДЮЪ§ЗжБ№ЮЊ8ЃЌ8,9ЃЌгЩЬтвт
ВЛЭЌЕФбЁШЁЗНЗЈга![]() ЙВ6жжЃЌ
ЙВ6жжЃЌ
ЩшЁАетСНУћЭЌбЇЕФЭЖРКУќжаДЮЪ§жЎКЭЮЊ17ЁБЮЊЪТМў![]() ЃЌдђ
ЃЌдђ![]() жаКЌга
жаКЌга![]() ЙВ2жжЛљБОЪТМў
ЙВ2жжЛљБОЪТМў
ЙЪ![]()

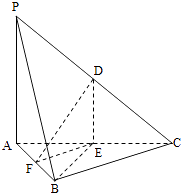
ЁОЬтФПЁПМзВЮМгA ЃЌ B ЃЌ CШ§ИіПЦФПЕФбЇвЕЫЎЦНПМЪдЃЌЦфПМЪдГЩМЈКЯИёЕФИХТЪШчЯТБэЃЌМйЩшШ§ИіПЦФПЕФПМЪдМзЪЧЗёГЩМЈКЯИёЯрЛЅЖРСЂЃЎ
ПЦФПA | ПЦФПB | ПЦФПC | |
Мз |
|
|
|
ЃЈIЃЉЧѓМзжСЩйгавЛИіПЦФППМЪдГЩМЈКЯИёЕФИХТЪЃЛ
ЃЈЂђЃЉЩшМзВЮМгПМЪдГЩМЈКЯИёЕФПЦФПЪ§СПЮЊX ЃЌ ЧѓXЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЁОЬтФПЁПвЛИіШнСПЮЊMЕФбљБОЪ§ОнЃЌЦфЦЕТЪЗжВМБэШчЯТЃЎ
ЃЈ1ЃЉМЦЫуa,bЕФжЕ;
ЃЈ2ЃЉЛГіЦЕТЪЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉгУЦЕТЪЗжВМжБЗНЭМЃЌЧѓГізмЬхЕФжкЪ§МАЦНОљЪ§ЕФЙРМЦжЕЃЎ
ЦЕТЪЗжВМБэ
Зжзщ | ЦЕЪ§ | ЦЕТЪ | ЦЕТЪ/зщОр |
(10,20] | 2 | 0.10 | 0.010 |
(20,30] | 3 | 0.15 | 0.015 |
(30,40] | 4 | 0.20 | 0.020 |
(40,50] | a | b | 0.025 |
(50,60] | 4 | 0.20 | 0.020 |
(60, 70] | 2 | 0.10 | 0.010 |