题目内容
【题目】如图,在三棱锥PABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证: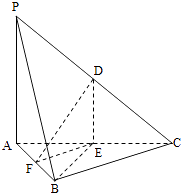
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
【答案】
(1)证明:∵D、E为PC、AC的中点,∴DE∥PA,
又∵PA平面DEF,DE平面DEF,
∴PA∥平面DEF;
(2)∵D、E为PC、AC的中点,∴DE= ![]() PA=3;
PA=3;
又∵E、F为AC、AB的中点,∴EF= ![]() BC=4;
BC=4;
∴DE2+EF2=DF2,
∴∠DEF=90°,
∴DE⊥EF;
∵DE∥PA,PA⊥AC,∴DE⊥AC;
∵AC∩EF=E,∴DE⊥平面ABC;
∵DE平面BDE,∴平面BDE⊥平面ABC.
【解析】(1)由中位线可得出DE∥PA,由线线平行,得出线面平行,(2)由中点及长度关系可得出DE=3,EF=4,由DE2+EF2=DF2,可知道∠DEF=90°,由DE∥PA,PA⊥AC,DE⊥AC;即DE⊥面ABC,即面BDE⊥面ABC.

练习册系列答案
相关题目