题目内容
【题目】已知直线l1：3x－2y－1＝0，直线l2：ax－by＋1＝0，其中a，b∈{1,2,3,4,5,6}．
(1)求直线l1∩l2≠的概率；
(2)求直线l1与l2的交点位于第一象限的概率．
【答案】（1）
（2）
【解析】试题分析： 
首先由直线
，直线
得出直线
和直线
的斜率，接下有由
可知总事件数为
，并由
，根据两条直线的斜率之间的关系，得到关于
的关系式，写出满足条件的事件数，即可得到结果；
首先由两条直线相交，联立方程组写出两条直线的交点坐标，接下来根据交点在第一象限得出关于交点坐标的不等式组，解出结果，即可得出答案。
解析：(1)直线l1的斜率k1＝
，直线l2的斜率k2＝
.
设事件A为“直线l1∩l2≠”．a，b∈{1,2,3,4,5,6}的总事件数为(1,1)，(1,2)，…，(6,6)共36种．若l1∩l2＝，则l1∥l2，即k1＝k2，即2a＝3b，满足条件的实数对(a，b)有(3,2)，(6,4)共两种情形．
∴P(A)＝1－
＝
，
则直线l1∩l2≠的概率为.
(2)设事件B为“直线l1与l2的交点位于第一象限”，由于直线l1与l2有交点，则2a≠3b.
联立方程组
解得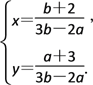
∵直线l1与l2的交点位于第一象限，则
即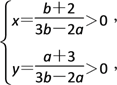
解得2a＜3b.
a，b∈{1,2,3,4,5,6}的总事件数为(1,1)，(1,2)，…，(6,6)共36种，
满足条件的实数对(a，b)有24种，
∴P(B)＝
＝
，
∴直线l1与l2的交点位于第一象限的概率为.
练习册系列答案
相关题目
