题目内容
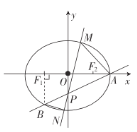
【题目】过点
的动直线l与y轴交于点
，过点T且垂直于l的直线
与直线
相交于点M.
（1）求M的轨迹方程；
（2）设M位于第一象限，以AM为直径的圆
与y轴相交于点N，且
，求
的值.
【答案】（1）
（2）4
【解析】
（1）动直线l过点
和
，可根据垂直求出直线
，从而求出交点M的坐标，从而寻找横纵坐标的关系，求出点M的轨迹方程. （2）由题意可知：点N即为圆与y轴的切点，根据
，可求出直线AM的斜率，进而求出直线AM的方程，从而求出
的值.
解：（1）∵，，当
时，M的坐标为
当
时，
，∴
，∴的方程为
由
得
，
验证当时，也满足
∴M的坐标满足方程，即M的轨迹方程为
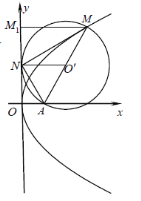
（2）作
轴于
，
轴于
，则
又A为抛物线的焦点，∴
，故圆
与y轴相切于点N
∵，∵
，∴
，∴直线AM的方程为
联立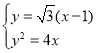
，消去y整理得
，解得
或
（舍），即
∵A为抛物线的焦点，∴
练习册系列答案
相关题目
【题目】为迎接“五一国际劳动节”，某商场规定购买超过6000元商品的顾客可以参与抽奖活动现有甲品牌和乙品牌的扫地机器人作为奖品，从这两种品牌的扫地机器人中各随机抽取6台检测它们充满电后的工作时长相关数据见下表（工作时长单位：分）
机器序号 | 1 | 2 | 3 | 4 | 5 | 6 |
甲品牌工作时长/分 | 220 | 180 | 210 | 220 | 200 | 230 |
乙品牌工作时长/分 | 200 | 190 | 240 | 230 | 220 | 210 |
（1）根据所提供的数据，计算抽取的甲品牌的扫地机器人充满电后工作时长的平均数与方差；
（2）从乙品牌被抽取的6台扫地机器人中随机抽出3台扫地机器人，记抽出的扫地机器人充满电后工作时长不低于220分钟的台数为
，求的分布列与数学期望.
