题目内容
【题目】如图,已知 ![]() 是上、下底边长分别为2和6,高为
是上、下底边长分别为2和6,高为 ![]() 的等腰梯形,将它沿对称轴
的等腰梯形,将它沿对称轴 ![]() 折叠,使二面角
折叠,使二面角 ![]() 为直二面角.
为直二面角.
(1)证明: ![]() ;
;
(2)求二面角 ![]() 的正弦值.
的正弦值.
【答案】
(1)证明:由题设知OA⊥OO1 , OB⊥OO1 , 所以∠AOB是所折成的直二面角的平面角,即OA⊥OB从而AO⊥平面OBCO1 , OC是AC在面OBCO1内的射影
因为tan∠OO1A= ![]() =
= ![]() ,tan∠O1OC=
,tan∠O1OC= ![]() =
= ![]() ,所以∠OO1B=60°,∠O1OC=30°,从而OC⊥BO1由三垂线定理得AC⊥BO1
,所以∠OO1B=60°,∠O1OC=30°,从而OC⊥BO1由三垂线定理得AC⊥BO1
(2)解:由(1)AC⊥BO1 , OC⊥BO1 , 知BO1⊥平面AOC
设OC∩O1B=E,过点E作EF⊥AC于F,连结O1F(如图),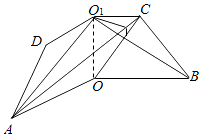
则EF是O1F在平面AOC 内的射影,由三垂线定理得O1F⊥AC所以∠O1FE是二面角O﹣AC﹣O1的平面角
由题设知OA=3,OO1= ![]() ,O1C=1,
,O1C=1,
所以 ![]() =2
=2 ![]() ,AC=
,AC= ![]() =
= ![]() ,从而
,从而 ![]() =
= ![]() ,
,
又O1E=OO1sin30°= ![]() ,所以sin∠O1FE=
,所以sin∠O1FE= ![]() =
= ![]() ,∴二面角O﹣AC﹣O1的正弦值为
,∴二面角O﹣AC﹣O1的正弦值为 ![]() .
.
【解析】(1)根据题意结合已知条件可得出∠AOB是所折成的直二面角的平面角,进而得出OA⊥OB再由线面垂直的判定定理可得AO⊥平面OBCO1 , 结合直角三角形的特点分别求出两个角的正切值,从而得到两个角的大小。(2) 由已知作出辅助线利用三垂线定理可得出∠O1FE是二面角O﹣AC﹣O1的平面角,利用勾股定理以及解三角形的知识求出其正弦值。

练习册系列答案
相关题目
