题目内容
某学校高一、高二、高三的三个年级学生人数如下表:
按年级分层抽样的方法评选优秀学生50人,其中高三有10人.
(1)求z的值;
(2)用分层抽样的方法在高一学生中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1名女生的概率.
(1)400;(2)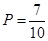 .
.
解析试题分析:(1)由高三总人数为400人,抽取10人,抽样比为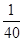 ,由此可求出三个年级的总人数,进而求出
,由此可求出三个年级的总人数,进而求出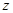 的值.
的值.
(2)由(1)知高一有女生400人,男生600人,用分层抽样的方法抽取一个容量为5的样本,其中女生2人,男生3人,可用古典概型得到所求的概率值.
解:(1)设该校总人数为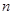 人,
人,
由题意,得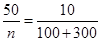 ,所以
,所以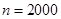 3分
3分
故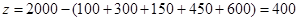 . 5分
. 5分
(2)设所抽样本中有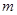 个女生.因为用分层抽样的方法在高一学生中抽取一个容量为
个女生.因为用分层抽样的方法在高一学生中抽取一个容量为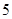 的样本,所以
的样本,所以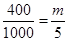 ,解得
,解得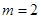 . 7分
. 7分
也就是抽取了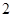 名女生,
名女生,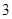 名男生,分别记作
名男生,分别记作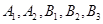 ,则从中任取
,则从中任取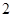 个的所有基本事件为(
个的所有基本事件为(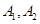 ),(
),(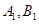 ),(
),(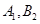 ),(
),(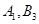 ),(
),(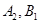 ),(
),(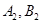 ),(
),( ),(
),(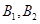 ),(
),(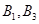 ),(
),(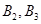 ),共10个; 9分
),共10个; 9分
其中至少有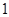 名女生的基本事件有
名女生的基本事件有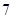 个: (
个: (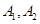 ),(
),(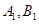 ),(
),(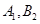 ),(
),(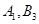 ), (
), (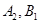 ),(
),(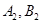 ),(
),( ) 11分
) 11分
所以从中任取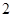 人,至少有
人,至少有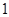 名女生的概率为
名女生的概率为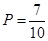 . 12分
. 12分
考点:1、分层抽样;2、古典概型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某普通高中共有教师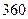 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 | 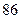 |  |  |
| 男教师 | 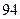 | 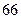 |  |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是
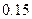 、
、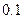 .
.(1)求
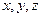 的值;
的值;(2)为了调查研修效果,现从三个批次中按
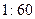 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?(3)若从(2)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
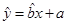 .
.(3)经计算,相关指数
 ,你可得到什么结论?
,你可得到什么结论?(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
为预防X病毒爆发,某生物技术公司研制出一种X病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 |  组 组 | 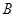 组 组 |  组 组 |
| 疫苗有效 | 673 | 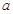 | 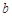 |
| 疫苗无效 | 77 | 90 | 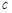 |
已知在全体样本中随机抽取1个,抽到
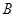 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33.(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在
 组抽取样本多少个?
组抽取样本多少个?(2)已知
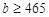 ,
,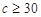 ,求通过测试的概率.
,求通过测试的概率. 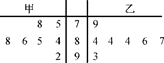


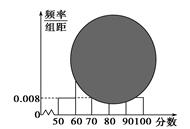
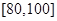 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在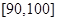 之间的概率;
之间的概率;
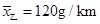 .
.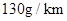 的概率是多少?
的概率是多少? 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.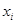 (年)与所支出的维修费
(年)与所支出的维修费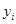 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果,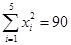 ,
,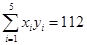 ,
,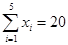 ,
,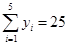 .
.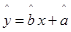 ;
;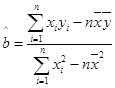 ,
,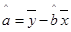 ,其中
,其中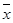 ,
, 为样本平均值.)
为样本平均值.)
 ,求甲在初赛中答题个数
,求甲在初赛中答题个数 的分布列及数学期望
的分布列及数学期望 .
.