题目内容
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
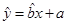 .
.(3)经计算,相关指数
 ,你可得到什么结论?
,你可得到什么结论?(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
(1)详见解析;(2)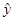 =7x+15;(3)详见解析.
=7x+15;(3)详见解析.
解析试题分析:(1)根据表格中的数据,易得散点图;(2)根据线性回归分析中的相关公式,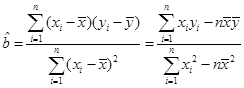 ,
, 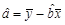 ,将表格中的数据代入,即可得到线性回归方程为
,将表格中的数据代入,即可得到线性回归方程为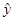 =7x+15;(3)相关指数R2是描述模拟效果好坏的一个量,它的值越接近于1,拟合效果越好,
=7x+15;(3)相关指数R2是描述模拟效果好坏的一个量,它的值越接近于1,拟合效果越好,
而对应的残差平方和就越小,在选择模型时,一般选择相关系大的模型,.
(1)根据条件中所给数据易得散点图如下图所示 4分
4分
(2)根据表格中数据, ,
, 8分
8分 =15, 10分
=15, 10分
∴线性回归方程为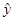 =7x+15. 11分
=7x+15. 11分
(3)本题要求学生根据相关指数R2的意义回答问题,结论叙述可以多样,如:
①相关指数R2接近1,说明模型拟合效果好;
②表明残差平方和接近0,说明模型拟合效果好;
③表明“解析变量和预报变量的线性相关性强”;
④表明“广告费支出解析了98%的销售额变化。而随机误差贡献了2%”,所以广告费支出
对销售额的效应比随机误差的效应大得多. 14分.
考点: 1、线性回归方程的求解;2、相关指数的应用.

以下是某地搜集到的新房屋的销售价格 (万元)和房屋的面积
(万元)和房屋的面积 (
(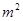 )的数据 ,若由资料可知
)的数据 ,若由资料可知 对
对 呈线性相关关系。
呈线性相关关系。
 | 80 | 90 | 100 | 110 | 120 |
| y | 48 | 52 | 63 | 72 | 80 |
试求:(1)线性回归方程;
(2)根据(1)的结果估计当房屋面积为
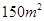 时的销售价格.
时的销售价格.参考公式:
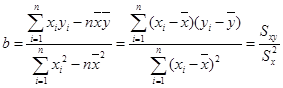
某中学一位高三班主任对本班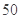 名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)学生的积极性与对待班级工作的态度是否有关系?说明理由.
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
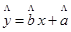
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于 小于
小于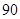 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利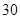 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 | 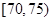 | 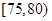 | 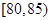 | 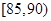 | 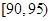 | 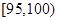 |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算甲生产一件产品A,给工厂带来盈利不小于30元的概率;
(2)若甲一天能生产20件产品A,乙一天能生产15件产品A,估计甲乙两人一天生产的35件产品A中三等品的件数.

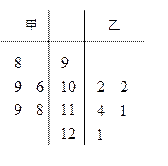
 ,
,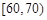 ,
, ,
,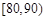 ,
,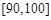 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
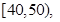
 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 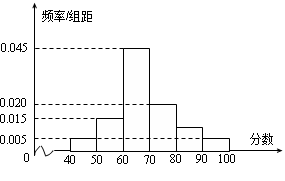
 的频率;
的频率;